Вращающаяся волна

Cтраница 1

Вращающаяся волна проходит через секцию с ферритом. При изменении подмагничивающего поля меняются намагниченность феррита, а следовательно, и его магнитная проницаемость [ формула ( 9 - 39) 1 Изменение магнитной проницаемости приводит к изменению фазовой скорости распространения волны в секции с ферритом, а следовательно, к изменению фазы колебаний на выходе фазовращателя. В деполяризаторе 2 вращающееся поле вновь преобразуется в линейно-поляризованное. [1]

Приближения вращающейся волны и медленно меняющихся амплитуд не могут быть приложены к уравнениям лазера в резонаторе, но они могут использоваться для упрощения лазерных уравнений, которые были выведены в разд. Поскольку такие упрощенные уравнения понадобятся намного позже, читатель может пропустить данный раздел и вернуться к нему тогда, когда это будет необходимо. [2]

Свое название приближение вращающейся волны получило из теории ядерного магнитного резонанса, где преобразование ПВВ (2.27) соответствует переходу в систему координат, вращающуюся вместе с магнитным полем. [3]

Рассмотрим сначала приближение вращающейся волны. [4]

При изменении тока соленоида распространение вращающейся волны в отрезке круглого волновода с ферритом сопровождается изменением фазы волны. Это объясняется тем, что с изменением магнитного поля изменяется магнитная проницаемость феррита и, следовательно, фазовая скорость распространения волны в отрезке волновода с ферритом. [5]

В дальнейшем мы примем приближение вращающейся волны, с которым мы уже познакомились в разд. А именно мы ограничимся рассмотрением реальных переходов, в которых испускается фотон, тогда как атом переходит из верхнего состояния в нижнее, или, напротив, фотон поглощается, а атом переходит из нижнего состояния в верхнее. [6]

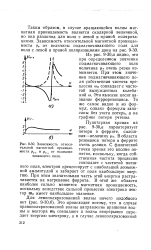Зависимость относительной магнитной проницаемости ( Jy и fj r от подмагни-чивающего поля. [7]

Таким образом, в случае вращающейся волны магнитная проницаемость является скалярной величиной, но она различна для волн с левой и лравой поляризациями. [8]

Поскольку мы с самого начала воспользовались приближением вращающейся волны, наш расчет будет правильно описывать динамику системы, но не даст правильной величины частотных сдвигов. [9]

Рассмотренный метод замены пульсирующей намагничивающей силы двумя вращающимися волнами удобен при определении намагничивающей силы многофазной обмотки. [10]

Легко понять, что в этой записи уже использовано приближение вращающейся волны. [11]

Пренебрежение членами, которые не сохраняют энергию, соответствует приближению вращающейся волны. [12]

К системе уравнений для зависящих от времени множителей применяется приближение вращающейся волны. Мы уже упоминали о нем в связи с пренебрежением нерезонансными членами при последовательном квантовом описании в разд. [13]

К такому виду при точном резонансе сводятся уравнения Блоха в приближении вращающейся волны ( см. разд. В нашем случае мы адиабатически исключили переменную дипольиого момента и получили уравнение для инверсии. [14]

Отметим, что в таком виде гамильтониан (9.2.21) записан без приближения вращающейся волны. [15]

Страницы: 1 2 3 4