Формула - симметрия
Cтраница 1
Формула симметрии состоит из записанных подряд всех элементов симметрии данного объекта. На первом месте принято писать оси симметрии от высших к низшим, на втором - плоскости симметрии, затем центр. [1]
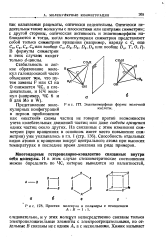 |
Энантиоморфные формы молочной кислоты.| Простая молекула и полимеры с отношением А. В 1. 1. [2] |
В формулы симметрии в этих случаях входят только d - циклы. [3]
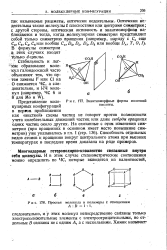 |
Энантиоморфные формы молочной кислоты. [4] |
В формулы симметрии в, этих случаях входят только d - циклы. [5]
В формулах симметрии приведены лишь основные элементы симметрии кристаллов разных классив. Так, в таблице не указывается ( кроме класса 1) элемент симметрии 1, который присущ всем классам; в тех случаях, когда приведена старшая по порядку ось, подчиненная ей младшая по порядку ось ( совпадающая по направлению) не указывается. Число осей и плоскостей в формулах симметрии записано в скобках. [6]
Полученные таким образом формулы симметрии возможных двойников срастания для каждого двойникового закона сведены в таблицу. [7]
Приведенные в скобках условные обозначения симметрии многогранника называют его формулой симметрии. [8]
В таблице 6.6 дан перечень этих групп с указанием их формулы симметрии, порядка группы и изоморфных групп, соподчиненно-сти группы. [9]
В табл. 3 приводятся наиболее распространенные в отечественной литературе обозначения ( формулы симметрии) и названия каждого вида симметрии, а также общепринятые международные символы по К. В этих обозначениях знака для осей симметрии нет, их заменяют на цифры ( порядок оси): 1 - Li; 2 - / 2; 3 - Ls; 4 - / 4 и 6 - Le. Если к оси четного порядка имеется перпендикулярная плоскость т, то это записывается так: 2 / т, 4 / / n, 6 / m; эти международные символы соответствуют формулам симметрии L2PC, LiPC и ЬЪРС. Международные символы не отличаются наглядностью, но они значительно компактнее и незаменимы для машинной техники. [10]
Остальные типы предельной симметрии мы получим деформациями сжатия и растяжения стержней, формулы симметрии которых записаны во втором столбце нашей таблицы. При деформации сжатия подгруппа конечных переносов ( а) заменяется подгруппой бесконечно малых переносов ( а), и мы переходим к типам симметрии третьего столбца. Эти типы описывают симметрию одномерных континуумов ( стержней, выполненных из сплошной среды), отличающихся от континуумов первого столбца произвольными ( в том числе бесконечно малыми) поворотами вдоль главной оси. [11]
 |
Ход циклов обмена, начиная с точки 7 как начальной. Симметрия оси - четвертого порядка. [12] |
Поскольку каждый отдельный символ цикла охватывает все эквивалентные точки, для получения формулы симметрии необходимо найденное выражение делить на число символов цикла. [13]
 |
Ход циклов обмена, начиная с точки 7 как начальной. Симметрия оси четвертого порядка. [14] |
Поскольку каждый отдельный символ цикла охватывает все эквивалентные точки, для получения формулы симметрии необходимо - найденное выражение делить на число символов цикла. [15]
Страницы: 1 2 3