Симметричный полосковый волновод
Cтраница 2
Индекс 1 относится к симметричному полосковому волноводу, а индекс 2 к несимметричному. [16]
 |
Конформное преобразование симметричного полоскового волновода. [17] |
Основным видом колебания в симметричном полосковом волноводе ( рис. 1.11 а), так же как и в несимметричном, является ТЕМ волна. [18]
Формулы для определения характеристического сопротивления симметричного полоскового волновода, так же как и формула (1.105) для несимметричного, справедливы для любых диэлектриков, применяемых на практике. Результаты расчетов - по формулам (1.101), (1.102) и (1.106) точнее совпадают с экспериментальными данными, чем по формулам характеристического сопротивления для несимметричных полосковых волноводов. В симметричных полосковых волноводах все пространство, занятое полем, практически заполнено однородным диэлектриком, чего нельзя сказать о несимметричных полосковых волноводах. [19]
Формулы для определения - характеристического сопротивления симметричного полоскового волновода, так же как и формула (1.105) для несимметричного, справедливы для любых диэлектриков, применяемых на практике. Результаты расчетов по формулам (1.101), (1.102) и (1.106) точнее совпадают с экспериментальными данными, чем по формулам характеристического сопротивления для несимметричных полосковых волноводов. В симметричных полосковых волноводах все пространство, занятое полем практически заполнено однородным диэлектриком, чего нельзя сказать о несиммет - ИЧБЫХ ГЮЛОСКОВЫХ волноводах. [20]
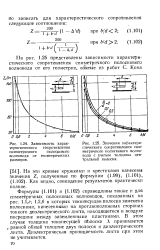
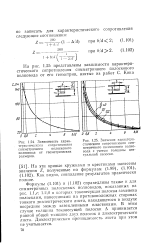
На рис. 1.25 представлены зависимости характеристического сопротивления симметричного полоскового волновода от его геометрии, взятые из работ С. [22]
Формулы (1.101) и (1.102) справедливы также и для симметричных полосковых волноводов, показанных на рис. 1.1 г; 1.2 6 в которых токонесущая полоска заменена полосками, нанесенными на противоположных сторонах тонкого диэлектрического листа, находящегося в воздухе посредине между заземленными пластинами. В этом случае толщина токонесущей пЪлоски А принимается равной общей толщине двух полосок и диэлектрического листа. Диэлектрическая проницаемость листа при этом не учитывается. [23]
Используя выражение (1.64), производится расчет напряженности поля симметричного полоскового волновода без учета толщины центральной полоски. [24]
Формулы (1.101) и (1.102) справедливы также и для симметричных полосковых волноводов, показанных на рнс. В этом случае толщина токонесущей полоски Д принимается равной общей толщине двух полосок и диэлектрического листа. Диэлектрическая проницаемость листа при этом не учитывается. [26]
Используя выражение (1.64), производится расчет напряженности поля симметричного полоскового волновода без учета толщины центральной полоски. [27]
Зная поле и поверхность поперечного сечения, можно легко найти мощность, передаваемую вдоль симметричного полоскового волновода. [28]
 |
Щелевой вибратор ( а и его эквивалентная схема ( б. [29] |
Более сложен вопрос конструирования щелевых по-лосковых антенн. Если проводимость излучения щели в экране симметричного полоскового волновода почти ке отличается от проводимости излучения щели в стенке прямоугольного волновода, то внутренние проводимости различаются значительно. [30]
Страницы: 1 2 3