Сферические волны

Cтраница 1

Сферические волны являются волнами растяжения - сжатия ( сферическими Р - волнами), так как в соответствии с (3.1.6), (3.1.15) и ( А. [1]

Сферические волны могут быть обусловлены наличием точечного центра расширения - сжатия в бесконечном упругом пространстве. Они могут возникнуть также в пространстве со сферической полостью, если на границе полости действует изменяющаяся во времени нагрузка. [2]

Сферические волны возбуждаются точечным источником волн или колеблющимся шаровым телом, размеры которого малы. Волновые поверхности сферической волны имеют вид концентрических сфер. По направлению любого радиуса сферы колебания происходят и распространяются совершенно одинаково. [3]

Сферические волны являются важным объектом изучения в электродинамике, поскольку с ними связаны многие задачи об излучении антенн. [4]

Эти сферические волны являются аналогом поперечных электрических ( ТЕ), или магнитных, цилиндрических волн. [5]

Две сферические волны, распространяющиеся от взаимно когерентных источников, интерферируют во всем пространстве. [6]

Две сферические волны излучаются точечными источниками Si и S. [7]

Мы рассмотрели только плоские и сферические волны, однако существуют и другие типы волн в волновыми фронтами иной формы. Но в любом случае две простые волны, складываясь, создадут на экране единственную в своем роде, присущую только этой паре волн интерференционную картину, которая зависит исключительно от параметров формирующих ее световых волн. [8]

Процесс распространения упругих волн. Если волны, выходящие из точки О, встречают на своем пути среду, где их скорость другая ( заштрихованная область на рисунке, происходит преломление волн. На верхнем рисунке изображен годограф для этого случая. [9]

ЭО, распространяются сферические волны. [10]

Возникающие за источником сферические волны, сливаясь друг с другом, образуют в пространстве коническую поверхность. Эта поверхность, разделяющая возмущенную движением источника часть среды от невозмущенной, является фронтом ударной волны. Ударные волны значительно отличаются от обычных звуковых волн. Они представляют собой распространяющуюся в пространстве область сильного сжатия среды и не имеют такого периодического характера, как звуковые волны. [11]

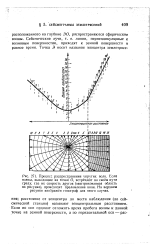
Например, две сферические волны на поверхности воды, распространяющиеся от двух когерентных точечных источников ( рис. IV.3.7), при интерференции дадут результирующую волну. [12]

Например, две сферические волны на поверхности воды, распространяющиеся от двух когерентных точечных источников ( рис. IV. [13]

Например, рассматривая сферические волны, возбужденные точечным источником, на достаточно большом удалении от него, можно из-за малой кривизны заменить малый участок сферы плоскостью. Другими словами, плоские волны являются предельным случаем сферических волн при стремлении радиуса сферы к бесконечности. [15]

Страницы: 1 2 3 4