Периодические волны

Cтраница 1

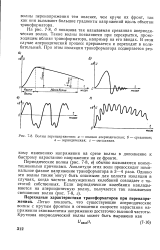Волны перенапряжения. а - полная апериодическая. б - срезанная. в - периодическая. г - смешанная. [1]

Периодические волны ( рис. 7 - 8, б) обычно вызываются коммутационными причинами. Амплитуда этих волн превосходит номинальное фазное напряжение трансформатора в 3 - 4 раза. Однако эти волны также могут быть опасными для целости изоляции в случаях, когда частота вынужденных колебаний совпадает с частотой собственных. [2]

Периодические волны - решения системы ( 25) вида ( 26), где w () есть периодическая функция. Периодические волны описываются уравпеная-ми распространения нервных импульсов и химической кинетики. [3]

Периодические волны в бесконечно глубоких каналах могут быть разобраны подобно периодическим волнам в каналах конечной глубины. Функционально-теоретическая задача при этом несколько упрощается. [4]

Периодические волны возбуждения могут быть получены и в диффузно организованной нервной ткани при ее электрическом раздражении. Они сходны с волнами возбуждения, возникающими в неанестезированной коре головного мозга в ответ на воздействие нескольких редких стимулов. Недавно был описан люминесцентный ответ у морских анютиных глазок ( вид цветного коралла): после серий раздражений эти колонии начали люми-несцировать спонтанно, а не только в ответ на стимуляцию. Для объяснения этого явления следует обратиться к механизму медленных изменений состояния нервной ткани ( элементарной форме памяти, связанной с медленными потенциалами. Эти изменения обусловлены влиянием окружающей среды и зависят, разумеется, от предшествующей активности организма. Но они также имеют свои внутренние закономерности и свой собственный ритм активности, который вызывает повторные изменения состояний нервной ткани, что делает их в каждый момент времени лишь частично зависимыми от влияний окружающей среды. [5]

Раздел 17.1. Подходящие периодические волны, посланные с противоположных концов пружины, могут образовывать узлы в определенных фиксированных точках при прохождении одной из этих волн сквозь другую. [6]

Так как все периодические волны можно описать посредством рядов Фурье как наложение синусоидальных волн, то рассмотрение чисто синусоидальной формы волны, очевидно, является простейшим случаем математической обработки. Другие переменнотоковые методы, в которых на постояннотоковую развертку напряжения налагается пилообразная, импульсная, квадратная, треугольная или какая-либо другая волна [2-7], могут быть рассмотрены теоретически с помощью более сложных функций Фурье или других методов. [7]

Все интегральные кривые описывают периодические волны конечной амплитуды. [8]

Предположим, что вы наблюдаете периодические волны, имеющие частоту / 4 колебания в секунду, сквозь двухщелевой стробоскоп. [9]

Особое место среди них занимают периодические волны. [10]

Точечный возбудитель вызывает в кювете круговые периодические волны. [11]

Следующий шаг состоит в том, чтобы использовать такие периодические волны для получения более общих ( нестационарных) решений. Очевидно, что в линейных задачах общее решение находят методом суперпозиции спектральных компонент. [12]

Наиболее изученными уравнениями, описывающими импульсы ( а также периодические волны, см. ниже), являются уравнения раепрострапения нервных импульсов - уравнения Ходжкипа-Хаксли и более простые уравнения Фитц-Хью - Нагумо. [13]

Фазовые кривые для уравнения ( ср. с. [14]

При этом сепаратрисы изображают солитоны, а остальные кривые - периодические волны. [15]

Страницы: 1 2 3