Нелинейные волны

Cтраница 2

Стохастические автоколебания в системе электронный пучок-обратная волна / / Нелинейные волны. Горький: Институт прикладной физики АН СССР, 1980, С. [16]

При А; 1 и А; 2 уравнение описывает нелинейные волны с осевой и центральной симметрией. [17]

Ленский ( 1981, 1982, 1983а, 1983Ь) рассмотрели нелинейные волны конечной амплитуды в изотропной ( q 0) упругой среде при различном выборе функции F. Магнитная гидродинамика идеально проводящих сред является, по существу, частным случаем теории упругости. Во всех перечисленных случаях, соответствующих равенству q О, поведение волн обладает определенными общими свойствами, обусловленными волновой изотропией. В частности, в случае волновой изотропии существуют, так называемые, вращательные волны для которых и2 г / 2 const. Они могут быть как непрерывными, когда они распространяются в виде бегущей волны в которой направление вектора [ и, и2 ] представляется произвольной функцией, так и разрывами с S О, распространяющимися с той же скоростью, что и непрерывные волны. [18]

Форма потенциальной ямы W ( ip согласно формуле для случая. FI О ( Т и FI О ( 2. [19]

Отметим, что уравнение КдВ справедливо для большого класса задач нелинейной физики, и нелинейные волны в электронных потоках часто описываются с его помощью. [20]

С математической точки зрения то, что мы получили, есть сведение цепочки с квадратичной нелинейностью к нелинейному уравнению с частными производными, которое описывает нелинейные волны малой амплитуды на больших пространственных отрезках. Примененный нами асимптотический метод перехода к непрерывному пределу носит название автомодельной редукции и широко применяется в математической физике. [21]

Уизема Линейные и нелинейные волны [72] есть раздел, начинающийся словами: По-видимому, не существует единого строгого определения волн. Можно дать различные частные определения, но чтобы охватить весь диапазон волновых процессов, предпочтительнее руководствоваться интуитивным представлением о волне как о любом различимом сигнале, передающимся от одной части среды к другой с некоторой определенной скоростью. Такой сигнал может быть возмущением любого вида, например, максимумом какой-либо величины или резким ее изменением при условии, что это возмущение четко выделено и что в любой заданный момент времени можно определить его местонахождение. Этот сигнал может искажаться, изменять свою величину и скорость, но при этом должен оставаться различимым. [22]

В дисперсионном решении (1.5) отношение амплитуд v / v0 равно аи0 / 2ул) 2 - U ( так называемый параметр Урселла), и если / велико. В результате возникают нелинейные волны или уединенные импульсы-солитоны. Эти вопросы кратко рассматриваются в гл. [23]

С нелинейными явлениями взаимодействия и самовоздействия волн все чаще приходится сталкиваться в современной лазерной оптике, акустике, физике плазмы. Нелинейные эффекты оказываются весьма существенными и при распространении мощных радиоволн в ионосфере. В современной физике волновых процессов нелинейные волны играют не менее важную роль, нежели нелинейные колебания в физике колебаний систем с сосредоточенными параметрами. [24]

Зависимость параметра / 3i от / 3 для симметричного нелинейного волновода показана на рис. 12.96, а энергетическая дисперсионная кривая Q ( / 3) - на рис. 12.9 а. Параметр / 3i на рис. 12.96 представлен для тех значений / 3, где он положителен. Напомним читателю, что это значит, что соответствующие нелинейные волны устойчивы. [25]

Разумеется, такие исследования далеко не полны. Однако оценка уже полученных данных подтверждает мысль о том, что нелинейные волны сохраняют высокую степень когерентности даже в двух измерениях. [26]

В первой главе рассматривается распространение волн с дисперсией в линейном приближении. Мы ограничились здесь изложением наиболее важных моментов, связанных с нелинейными обобщениями, которые обсуждаются в дальнейшем. Во второй главе рассматриваются некоторые характерные примеры диспергирующих сред и выясняются общие особенности уравнений, описывающих нелинейные волны в таких средах. Третья глава посвящена изучению стационарных волн. В четвертой главе излагается теория нелинейных волн со слабой дисперсией. Здесь выводятся и исследуются уравнения Бюргерса и Кортевега - де Вриза, которые применяются затем к ряду конкретных задач. В пятой главе рассматриваются основы адиабатической теории нелинейных волн и нелинейное параболическое уравнение. [27]

Рассматривается решение сферически симметричной системы уравнений Эйлера. Решается задача о пульсирующем поведении сферы в сжимаемой среде. При этом для точного численного решения требуются граничные условия на искусственной границе, которые моделировали бы распространение нелинейных волны без отражения от границ. Представлены нелинейные неотражающие адаптивные граничные условия, которые обеспечивают уменьшение отражения от искусственных границ по сравнению с классическими локальными граничными условиями для волновых уравнений. Нелинейная процедура позволяет значительно улучшить точность граничных условий, даже если исходные уравнения являются линейными. Обсуждаются работы, в которых детально рассматривалась численная реализация простых условий ( экстраполяция нулевого и первого порядков) на границах расчетной области при моделировании уравнений Навье-Стокса. Рассматривается модификация неотражающих граничных условий при газодинамическом моделировании в астрофизике. [28]

Выражения ( 56) и ( 57) показывают, что как скорость, так и форма волны зависят от амплитуды возмущения и параметров невозмущенного состояния, на фоне которого распространяется волна. Появление зависимости от амплитуды - это, очевидно, особенность, обусловленная нелинейностью. В отличие от обсуждавшейся в гл I и II строго линейной ( частотной) дисперсии, связанной с длиной волны, зависимость скорости от амплитуды названа амплитудной дисперсией. Конечно, необходимо помнить, что нелинейные волны, вообще говоря, не подчиняются принципу суперпозиции. [29]

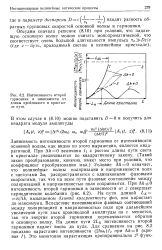Интенсивность второй гармоники в зависимости от длины пройденного в кристалле пути. [30]

Страницы: 1 2 3