Фазовые волны

Cтраница 1

Фазовые волны ( в противоположность триггерным) не обладают однозначно определенной скоростью распространения. [1]

В случае фотонов фазовые волны совпадают по направлениям и скоростям со световыми, но, отождествляя их, мы пришли бы к непреодолимым противоречиям, В остальных случаях фазовые волны имеют скорость, превышающую скорость света г, и уже по одному этому не могут быть ни электромагнитными волнами в эфире, ни волнами какого-нибудь иного материального субстрата: по теории относительности ни одно реальное перемещение в пространстве не может совершаться быстрее скорости света. Формально конечно можно, как это часто и делают, считать фазовые волны волнами вероятности, но это ничего не дает для их физического понимания, все еще от нас ускользающего. Возможно, что фазовые волны вообще не составляют непосредственной физической реальности, а служат лишь средством описания более сложных, неизвестных нам еще процессов. [2]

При этом ему сопутствуют фазовые волны таким образом, что орбита электрона является их ортогональной траекторией или лучом. [3]

В этом смысле я истолковываю фазовые волны, сопровождающие согласно де Бройлю движущийся электрон; в этом же смысле не имеет какого-либо особого значения, во всяком случае в атоме, траектория электрона и тем более его положение на этой траектории. [4]

При отражении от диффракционной решетки фазовые волны должны подвергаться той же диффракции, как и любые другие волны, встречающие препятствия на своем пути. При этом фазовая волна отклоняется от своего пути, вместе с чем отклоняется и та частица, которой она принадлежит. Так как фазовая волна является свойством самой частицы ( а быть может даже лишь способом ее описания), то можно говорить в данном случае о диффракции самих электронов. Поэтому для диффракции электронов должны быть особенно пригодны те же кристаллические решетки, которыми вызывается, как мы видели, диффракция рентгеновских лучей. [5]

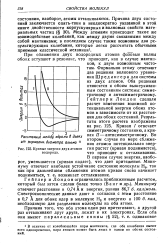Кривые энергии двух атомов водорода. [6]

При сближении двух водородных атомов фазовые волны обоих вступают в резонанс, что приводит, как в случае маятников, к двум возможным частотам. Формально этому отвечают два решения волнового уравнения Шредингера для системы из двух атомов. Оба решения относятся к обоим вышеуказанным состояниям системы: симметричному и антисимметричному. Гейтлери Лондон сделали расчет изменения взаимной потенциальной энергии обоих атомов в зависимости от их расстояния для обоих состояний. [7]

Фазовые волны иногда называют волнами материи, электронными вод-нами иди ведущими волнами. [9]

Классическая механика соответствует геометрической оптике фазовых волн с определенными лучами, которым отвечают точно фиксированные траектории материальных частиц. Между тем легко видеть, что фазовые волны имеют длины одного порядка с размерами атомов и их составных частей, между которыми они распространяются. [10]

Отсюда естественно вытекает возможность применения их не только к гипотетическим световым квантам, но и к настоящим материальным частицам и, прежде всего, к элементарным частицам материи - электронам. При этом фазовые волны де Бройля утрачивают всякое сходство и вообще всякую связь с обыкновенными электромагнитными волнами классической электродинамики. Согласно последней, электрон, движущийся прямолинейно и равномерно, никаких волн не создает. Фазовые волны, сопутствующие электрону или несущие его на своем гребне, имеют совершенно иной, притом скорее чисто механический, нежели электромагнитный смысл. [12]

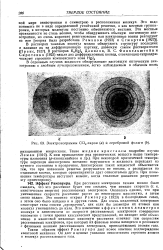Электронограммы СС14 - паров ( а и серебряной фольги ( Ь. [14]

Оказалось однако, что при уменьшении скорости рассеяние растет до некоторого максимума, а затем снова падает. Это явление открыл Р а м з а у е р ( 1923) в благородных газах, а затем оно было найдено и в других газах. Для очень медленных электронов некоторые газы совсем прозрачны, как если бы диаметры их атомов или молекул уменьшались до нуля. Эго изменение эффективных диаметров молекул в зависимости от скорости рассеиваемых электронов совершенно непонятно с точки зрения классических представлений, но находит себе объяснение в квантовой механике: максимум рассеяния отвечает тем скоростям рассеиваемых электронов, при которых их фазовые волны находятся в резонансе с фазовыми волнами рассеивающих электронов, принадлежащих атомам газа. [15]

Страницы: 1 2