Цилиндрические волны

Cтраница 1

Цилиндрические волны рассматриваются в задачах электродинамики, связанных с излучением электромагнитных волн отрезками линейных проводников. [1]

Цилиндрические волны могут возникнуть в случае линейного источника тепла или линейного центра расширения - сжатия и в неограниченной термоупругой среде с цилиндрической полостью, на границе которой задан нагрев, давление или деформация, распределенные осесимметричным образом. [2]

Краевые цилиндрические волны, возникающие в модельной задаче о падении плоской волны на клин, могут трактоваться как особого вида лучевое поле, как мы уже упоминали в начале параграфа. Лучи от ребра клина порождаются лучами, падающими на ребро. Эти новые лучи, носящие название дифракционных, ведут себя после своего возникновения точно так же, как обычные геомет-рооптические лучи. Отличие заключается в законах, которым подчиняется образование дифракционных лучей. [3]

Рассмотрим цилиндрические волны для случая, когда перемещение и температура зависят только от переменных гит. Эти волны могут возникать под действием линейного источника или же в неограниченной среде с цилиндрической полостью, на поверхности которой заданы равномерно распределенное давление, тепловой поток или деформация. [4]

Преломление волн диэлектрической линзой. [5]

В цилиндрических линзах цилиндрические волны преобразуются в плоские. [6]

Вычисляя эти интегралы методом перевала, получим две цилиндрические волны, фазы которых отличаются на у и мощности поэтому просто складываются. [7]

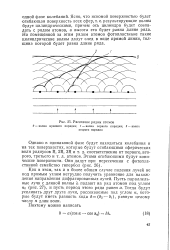Рассеяние рядом атомов. [8]

На помещенной за этим рядом атомов фотопластинке такие цилиндрические волны дадут след в виде прямой линии, толщина которой будет равна длине ряда. [9]

Уравнение ( 173) есть волновое уравнение для плоского случая ( цилиндрические волны), но, пользуясь принципом наложения, можно из решений указанного выше типа составлять новые решения и исследовать таким образом волновое уравнение и в общем случае трехмерного пространства. [10]

Уравнение ( 191) есть волновое уравнение для плоского случая ( цилиндрические волны), но, пользуясь принципом наложения, можно из решений указанного выше типа составлять новые решения и исследовать таким образом волновое уравнение и в общем случае трехмерного пространства. Не вдаваясь в подробности, которые завели бы нас слишком далеко и потребовали бы много места, мы изложим весьма кратко применение этого метода к двум задачам: к задаче диффракции плоской волны и к задаче отражения упругих колебаний от плоской границы. [11]

Легко проверить, что под действием линии центров сжатия возникают лишь продольные цилиндрические волны. [12]

Эти выражения показывают, что от края полуплоскости расходятся во все стороны цилиндрические волны. [13]

В обоих случаях из открытого конца волновода расходятся не сферические, а цилиндрические волны, распространяющиеся между параллельными плоскостями, поэтому нельзя судить по результатам решения задач, относящихся к системам, приведенным на рис. 17 и 18, о прямоугольном волноводе, открывающемся в свободное пространство. Заметим, в частности, что в системе, показанной на рис. 17, открытый конец волновода ведет себя как индуктивная нагрузка, а в системе рис. 18 - как емкостная. Таким образом, расположение добавочных плоскостей коренным образом меняет характер отражения от колца волновода. [14]

В силу формул (10.05) выражения для Е х и Е х суть цилиндрические волны, расходящиеся соответственно от края верхней и нижней пластины волновода. [15]

Страницы: 1 2 3