Вольфсберг

Cтраница 2

Заряды на каждом атоме, обычно рассчитываемые в модели Вольфсберга - Гельмгольца, должны быть самосогласованы. Это означает, что окончательные значения Kt должны давать полные заряды на центральном атоме и лигандах, согласующиеся со значениями q и q -, использованными для расчета Яг. Несмотря на многочисленные недостатки такого рода, метод Вольфсберга - Гельмгольца часто полезен при интерпретации спектров. [16]

Удивительно простой метод, предложенный Хюккелем для сопряженных молекул [29] и примененный Вольфсбергом и Гельмгольцем к неорганическим комплексам [30], был распространен Хоффманом [31] на все углеводороды и впоследствии - на все органические и неорганические системы. [17]

Количественные вычисления, основанные на этой теории, проводили Фридман, Лонг и Вольфсберг [7]; Коллин [8] и Кропф [9] - для сравнительно простых молекул. Фридман и соавторы вычислили масс-спектры метанола, этанола и бутанолов, считая эти системы совокупностью осцилляторов, при минимальном количестве полуэмпирических самосогласующихся величин для зависящих от частоты параметров в выражении для константы скорости. Из качественных приложений этой теории и энергетических рассмотрений установлен механизм образования тех осколочных ионов, число которых превышает 3 % от общего количества ионов. Ещах возрастает от 7 до 9 - 12 эв с усложнением молекулы спирта. Результаты вычислений Коллина для этилгалогенов этилового спирта, этиламина и этилмеркаптана, в которых учитывалось изменение масс-спектра с изменением энергии электронов, хорошо согласуются с экспериментом. [18]

Результаты для кубической группы получены Ван Флеком [191], Оргелом 1147 ] и Вольфсбергом и Гельмгольцем [202], и мы не будем воспроизводить их здесь. [19]

В настоящей главе приведена программа расчета электронного строения соединений переходных элементов методом Малликена - Вольфсберга - Гельмгольца с самосогласованием по зарядам и конфигурациям. Программа позволяет автоматически учесть симметрию рассматриваемой системы: расчеты выполняются в базисе орбиталей симметрии. Программа оформлена в виде двух независимых частей: программы вычисления групповых интегралов перекрывания и программы собственно метода МЯГ. Очевидно, при соответствующем задании исходной информации программы могут работать и в режиме расчетов в базисе обычных АО, однако быстродействие программы МВГ в этом случае заметно снижается - время расчета может существенно возрасти. [20]

Этот изотопный эффект более чем вдвое сильнее полученного с помощью уравнений Бигеляйзена и Бигеляйзена - Вольфсберга. [21]

Другой способ оценки параметра Р основан на данных УФ-спектроскопии сопряженных систем в сочетании с методом Вольфсберга - Гельмгольца. [22]

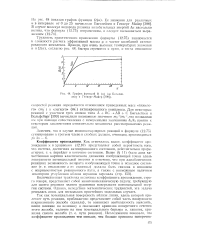График функций и ( и ( по Бигелей-зеиу и Гепперт-Майер. [23]

Для некоторых реакций с участием трех атомов типа А ВС - - АВ С Бигелейзен и Вольфсберг [399] вычислили возможные значения тп2 / / п что позволило им при помощи сопоставления с измеренными значениями k / k2 прийти к некоторым заключениям относительно механизма рассматриваемых реакций. [24]

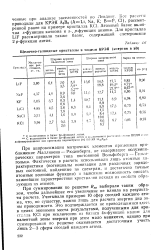Щелочно-галоидные кристаллы в модели КРЭЯ ( энергия в эВ. [25]

При аппроксимации матричных элементов применяли приближение Малликена - Рюденберга, не содержащее полуэмпирических параметров типа постоянной Вольфсберга - Гельм-гольца. Фактически в расчете использовали лишь атомные характеристики ( потенциалы ионизации для различных зарядовых состояний, найденные по спектрам, и достаточно точные атомные волновые функции) и выясняли возможность описать важнейшие характеристики кристаллов исходя из свойств образующих их атомов. [26]

Хотя, учитывая возможность наличия большого заряда на атоме металла, такое упрощение заведомо нельзя применять для оценки диагональных элементов f, L, соответствующих АО лигандов, оно часто использовалось в ранних расчетах МО соединений переходных металлов по методу Вольфсберга - Гельмгольца. [27]

Трудности неэмпирических расчетов породили еще более простые ( чем методы НДП) чисто полуэмпирические методы расчета, из которых наибольшее распространение в применении к координационным соединениям получил метод МВГ. Первоначальная идея, предложенная Вольфсбергом и Гельмгольцем [138], сводилась к тому, чтобы в секулярном уравнении метода МО ЛКАО ( V. [28]

Зельтцер [112], исходя из экспериментальных данных, приводит убедительные доказательства в пользу того, что для таких реакций замедления порядка 12 % являются обычными. При этом он ссылается на Вольфсберга, который на основании теоретических соображений считает, что эффект появления заряда должен играть второстепенную роль. Примем далее на основании результатов Дени и Танкеля [100] ( отнесенных к реакции у одного атома углерода), что такая же величина изотопного эффекта характерна для превращения аналогичного по строению переходного состояния в плоскотригональную конфигурацию. [29]

В этом варианте матричные элементы вычисляются по (3.20), однако вводится зависимость их от заряда и конфигурации электронов на атоме А. Этот метод известен в литературе также под названием метода МВГ ( Малликена - Вольфсберга - Гельмгольца) и был впервые применен в расчетах комплексов переходных металлов. [30]

Страницы: 1 2 3