Вопрос - распространение - волна
Cтраница 1
Вопросы распространения волны в реальных акустических преобразователях ультразвуковых приборов тесно связаны с наличием и характером преломляющих поверхностей преобразователя. [1]
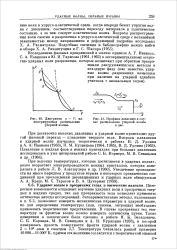 |
Диаграмма р - F, иллюстрирующая расщепление ударной волны.| Профиль давления в случае расщепления ударной волны. в две. [2] |
Вопросы распространения волн сжатия и разрежения в упруго-пластической среде с нелинейной зависимостью между напряжением и деформацией подробно исследовал X. [3]
Вопросам распространения волн в предварительно напряженных неограниченных телах посвящено большое количество работ отечественных и зарубежных авторов. Основное внимание уделено исследованию закономерностей распространения объемных волн [ 50, 53, 54, 63, 64, 73, 79, 92, 98, 103 - 107, ПО, 111, 116, 119, 120, 126 - 129, 134 - 137, 145, 151 - 155, 157 - 159, 164 - 170, 174, 179, 180, 183 - 188, 192 - 198 201 - 210 212 - 214 218, 220 - 232, 235 - 239, 241, 243, 248, 251 и др. ], на основе которых возможна разработка экспериментальных, основанных на использовании закономерностей распространения проходящих или отраженных волн, методов оценки напряженного состояния деталей и узлов конструкций, находящихся в условиях воздействия силовых факторов различной природы. [4]
Из вопросов распространения немонохроматической волны представляет определенный интерес один частный случай: взаимодействие двух волн, распространяющихся в одном направлении. [5]
При рассмотрении вопросов распространения волн очень удобным и наглядным является представление о луче. Лучом называют линию, касательная к которой в каждой точке совпадает с направлением распространения волны в этой точке. Так, в случае распространения плоской волны в однородной среде лучами являются прямые, нормальные к фронту волны. При преломлении волн на границе двух сред направление лучей измеряется. В неоднородной среде, свойства которой в разных местах различны, фронт волны может постепенно поворачиваться по мере распространения, и тогда лучи будут представлять собой некоторые кривые. Только для плоской волны в однородной среде направление лучей в разных участках волны будет одно и то же; в других случаях оно для разных участков волны, вообще говоря, различно. [6]
При рассмотрении вопросов распространения волн очень удобным и наглядным является представление о луче. Лучом называют линию, касательная к которой в каждой точке совпадает с направлением распространения волны в этой точке. Так, в случае распространения плоской волны в однородной среде лучами являются прямые, нормальные к фронту волны. При преломлении волн на границе двух сред направление лучей изменяется. В неоднородной среде, свойства которой в разных местах различны, фронт волны может постепенно поворачиваться по мере распространения, и тогда лучи будут представлять собой некоторые кривые. Только для плоской волны в однородной среде направление лучей в разных участках волны будет одно и то же; в других случаях оно для разных участков волны, вообще говоря, различно. [7]
 |
Распространение поверхностной и пространственной волн. [8] |
При рассмотрении вопроса распространения волн различной длины используют понятие о поверхностных ( земных) и пространственных волнах. [9]
В этой главе рассматриваются некоторые вопросы распространения волн в пла-нарных нелинейных волноводах и их устойчивость. Нелинейные поверхностные волны представляют собой самосфокусированные пучки, которые распространяются вдоль границы раздела линейной и нелинейной сред, причем коэффициент отражения в линейной среде должен быть больше, чем константа в степенном разложении коэффициента преломления в нелинейной среде. Хотя существование нелинейных поверхностных волн с физической точки зрения легко объяснимо, их свойства далеко не тривиальны. Первый вопрос, с которого следует начать изучение нелинейных волноводов - нахождение стационарных решений для данной геометрии волновода. [10]
Этот принцип, так называемый принцип Гюйгенса - Френеля, широко применяется для рассмотрения вопросов распространения волн. [11]
В этом параграфе будут рассмотрены основы теории для изотропного твердого тела без потерь, а также очень кратко некоторые вопросы распространения волн конечной амплитуды в кристаллах. Заметим, что в отличие от рассмотрения газов и жидкостей, когда преимущественно выбирают эйлеровы координаты, шри рассмотрении твердых тел, как правило, используют лагранжеву систему координат. [12]
Эта возможность замены любого реального источника системой точечных источников, интерферирующих между собой, подсказывает идею важного принципа, применяемого при рассмотрении вопросов распространения волн. [13]
В седьмом томе последовательно рассмотрены теория упругости анизотропного тепа, критерии прочности композиционных материалов, метод расчета стержней, пластин, оболочек, элементов конструкций и узлов их соединений, вопросы распространения волн в конструкциях из композиционных материалов. Приведен обширный экспериментальный материал. [14]
В книге дан обзор известных методов статистической динамики, обоснованы вариационные методы исследования, приведены прикладные задачи и инженерные методы расчета дискретных колебательных систем, и также статические и динамические задачи для упругих конструкций ( балок, пластин, оболочек), вопросы распространения волн в стохастически неоднородных средах. [15]
Страницы: 1 2