Большой ансамбль

Cтраница 3

Иными словами, при движении снизу к р макромолекулы достигают такой степени развернутости, что им оказывается выгодным развертываться дальше, ибо энергия Гиббса становится при этих условиях ниже, если взаимодействие сегментов осуществляется с сегментами других цепей. С этим переходом, который нетрудно наблюдать на опыте и который можно назвать переход клубок-развернутая цепь, связано скачкообразное изменение кинетических, термодинамических и морфологических свойств уже большого ансамбля макромолекул. [32]

Без компенсации этой энергии наблюдать резонансное поглощение гамма-квантов невозможно. Поскольку для кристаллов ширина резонансной линии на 10 порядков меньше, чем для газов, в которых отдачу испытывает отдельное ядро, то, чтобы избавиться от отдачи, нужно перейти от единичных ядер к большому ансамблю ядер в виде кристалла. Возникающие в такой системе процессы называют поглощением гамма-квантов без отдачи, что и характеризует сущность эффекта Мессбауэра. [33]

Вместо того, чтобы рассматривать, как в предыдущих главах, ансамбли систем, отличающихся только фазами, мы будем предполагать в дальнейшем, что системы, составляющие ансамбль, состоят из частиц различных видов, и что они отличаются не только фазами, но также и числами содержащихся в них частиц. Внешние координаты всех систем ансамбля предполагаются, как и ранее, имеющими одинаковое значение и, когда они изменяются, изменяющимися совместно. Большой ансамбль, следовательно, состоит из множества малых ансамблей. Ансамбли, которые мы исследовали до сих пор, являются малыми ансамблями. [34]

Они выражаются через приведенные матрицы плотности из соотношений (6.4.1), которые теперь имеют смысл условий самосогласования. Наиболее подробное описание начального состояния соответствует тому, что все приведенные матрицы плотности рассматриваются как независимые параметры состояния. Тогда в большом ансамбле оператор S содержит бесконечное число членов. Ясно, что в этом случае практически невозможно решить, даже приближенно, уравнения для множителей Лагранжа. Поэтому приходится ограничиваться модельными выражениями для S, содержащими конечное число членов. Достаточно простое и во многих случаях физически разумное описание начального состояния с многочастичными корреляциями дает модель, в которой независимыми параметрами являются одночастичная и двухчастичная матрицы плотности. [35]

В настоящей статье мы хотели бы показать, во-первых, как используется термодинамический метод Гиббса для трактовки тонких слоев, никакая часть которых, в отличие от случаев, рассмотренных Гиббсом, не обладает свойствами объемной фазы. Показано, что в этом случае вследствие перекрытия межфазных переходных слоев возникает новый мир явлений, определяющий основные свойства дисперсных систем. Во-вторых, в статье указывается на применение большого ансамбля Гиббса, с одной стороны, и работы образования критического зародыша новой фазы, с другой, или строгого вывода вероятности образования новой фазы. [36]

Книга содержит четыре главы. В главе I излагаются осно закономерности теории нуклеации в гомогенных и гетероге системах. Методической основой этой главы является исполь ние большого ансамбля Гиббса для процесса ния. В этой же главе рассматривается влияние на образование и свойства тонких слоев. [37]

Поскольку К имеет тот же порядок величины, что и число молекул в обычных телах, это выражение определяет, очевидно, величину столь малую, что ею можно пренебречь. Необходимо отметить, что % еп представляет собой здесь среднее по большому ансамблю, тогда как величина, которую мы желаем сопоставить с Я, является средней по малому ансамблю. Однако, поскольку мы видели, что в рассматриваемом случае большой ансамбль представляется человеческому наблюдению одинаковым с малым ансамблем, то этим отличием можно пренебречь. [38]

Тот факт, что между коллоидными частицами существуют силы притяжения, был установлен еще в начале этого столетия Смолуховским по кинетике коагуляции золей. Однако, как показали Де Бур и Га-макер, для макроскопических тел, например коллоидных частиц, состоящих из многих тысяч атомов ( молекул), эти силы складываются, в результате чего суммарная энергия притяжения частиц изменяется гораздо медленнее - по кубическому или квадратичному закону. Иначе говоря, эти силы в определенных условиях достаточно велики и соизмеримы с силами отталкивания двойных электрических слоев. Основной вклад в молекулярное притяжение дисперсных тел вносят силы дисперсионного взаимодействия ( лондоновские силы), так как ориентационные и индукционные эффекты отдельных молекул для достаточно большого ансамбля взаимно компенсируются. [39]

Ни в одной из рассмотренных ранее молекулярных теорий разрушения ( разд. Конечно, первые разрывы большого ансамбля первоначально равномерно напряженных молекул будут происходить случайно. Еще более высокая плотность вероятности разрыва присуща небольшому числу элементов, расположенных вблизи уже имеющихся очагов разрушения. Так что ( суммарная) вероятность разрыва одного такого элемента, до этого момента не затронутого разорванным элементом, вначале меньше вероятности разрыва одной цепи из большого ансамбля. С ростом их числа возрастает вероятность разрывов в непосредственной близости от уже имеющихся, благодаря чему формируются зародыши трещины и повышается вероятность разрушения соседних элементов. [40]

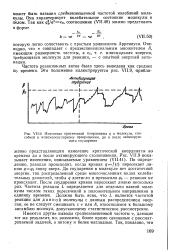Изменение критической координаты q в молекуле, способной к мономолекулярному превращению, до и после активирующего соударения. [41]

По определению, реакция происходит, когда кривая qf ( t) пересекает линию 7 7о снизу вверх. До соударения в молекуле нет достаточной энергии, так распределенной среди многочисленных видов колебательных движений, чтобы q достигло и превысило 7о - реакция не происходит. После соударения кривая пересекает линию несколько раз. Частота реакции L определяется для отдельно взятой молекулы числом таких пересечений в положительном направлении в единицу времени. Должно быть ясно, что L является частотой реакции для данной молекулы с данным распределением энергии; ее не следует смешивать с v или А, относящимся к большому ансамблю молекул, допускающему статистическое рассмотрение. [42]

Часто связь между соседними частицами бывает настолько сильной, что теория локализованного экситона оказывается уже неприменима. Сильная связь приводит к расщеплению уровней энергии возбужденных состояний. Взаимодействие частиц в основном состоянии содержит только вандервааль-совы члены и приводит, таким образом, обычно только к понижению уровня основного состояния без расщепления его. Аналогичный вандерваальсов сдвиг наблюдается и для возбужденного состояния. Но дополнительно имеется также расщепление уровней, вызванное кулоновским и обменным взаимодействиями ( давыдовское расщепление) между соседними молекулами. Это приводит к необходимости рассматривать волновую функцию для большого ансамбля взаимодействующих молекул - в некотором смысле одной гигантской молекулы - вместо волновой функции отдельной молекулы. Такая волновая функция составляется в виде линейной комбинации идентичных волновых функций отдельных молекул. В результате при включении в рассмотрение N молекул один уровень расщепляется в полосу тесно расположенных N уровней. Подобные уровни представляют собой уровни энергии кристалла как целого. В результате нам приходится иметь дело с гигантской молекулой, а не с упорядоченным множеством отдельных осцилляторов. Поглощает энергию кристалл как целое. Такая трактовка дается теорией делокализованного экситона. [43]

Страницы: 1 2 3