Вывод - функция - распределение
Cтраница 1
Вывод функции распределения, таким образом, завершен. [1]
Однако вывод функции распределения менее громоздок в случае реакции ( I), так как в ней принимает участие только один мономер. Поэтому вывод функции распределения будет проведен на примере именно этой, реакции. Если проделать те же выкладки для случая реакции ( II), то получается практически тот же результат. [2]
При выводе функции распределения необходимо учитывать симметричность дерева относительно вершив типа Лг1, таи как в противном случае одни и те же структурные модификации дерева учитываются дважды. [3]
При выводе функции распределения ( по Флори18) обозначим через Мх молекулу Н ( - NH-CHR-CO -), - R, а через Mi-молекулу инициатора R H. [4]
Поскольку при выводе функции распределения используется модель свободно-сочлененной цепи, то, очевидно, предполагается, что изменение конформации макромолекулы не сопровождается изменением внутренней энергии. Отсюда следует, что при деформации свободно-сочлененной цепи ( например, при растяжении) изменение ее свободной энергии полностью обусловлено изменением ее энтропии. [5]
Применим данный метод для вывода функции молекулярно-мас-сового распределения ( МИР) полимера, полученного по свободно-радикальному механизму. Рассматриваемая кинетическая схема учитывает реакции внутри - и межмолекулярной передачи цепи, приводящие к образованию двух типов разветвленности, передачу цепи на мономер и любой низкомолекулярный продукт, обрыв цепи путем диспропорционирования. Эта схема применима, например, при описании процесса полимеризации этилена. [6]
Целесообразно, прежде чем перейти к выводу функции распределения макромолекул, рассмотреть распределение макрорадикалов по длинам цепи. Доля последних обычно крайне низка и за исключением начального момента процесса пренебрежимо мала по сравнению с долей неактивных макромолекул. Строго говоря, в распределении по молекулярной массе учитываются и те и другие макромолекулы, но обычно вкладом радикалов пренебрегают. В то же время удобно вначале рассчитать функцию распределения именно для радикалов с тем, чтобы использовать полученный результат для расчета функции распределения макромолекул. [7]
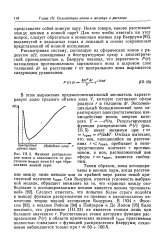 |
Функция распредели ИОНОМ а ион расположенный вне ния ионов в зависимости от рас - Сферы Т Гкрит, является СВОбод-стояния между ними ( г при обра - ным. [8] |
Следует отметить, что попытки более строго подойти к выводу функции распределения не привели к кардинальному изменению теории ионной ассоциации Бьеррума. В 1934 г. Фуос-сом [93], а позднее Рейсом [94] и Пойрером и Де Лапом [95] было показано, что уравнение ( III. Рассчитанные этими авторами функции распределения Р ( г) в области критических значении гкрит практически полностью совпадают с функцией распределения Бьеррума; отклонения наблюдаются только при г 50 - т - 100 А. [9]
Это свойство функций распределения отдельных компонент скорости априори было положено Максвеллом в основу вывода функции распределения для стационар-ного однородного состояния газа. [10]
Поскольку понятия гауссовых ансамблей играют исключительно важную роль, далее будет приведен еще один вывод функции распределения матричных элементов. [11]
Величину [ R ] мы можем получить, решая первое из уравнений ( 32 - 23), но для вывода функции распределения этого не требуется. [12]
Однако вывод функции распределения менее громоздок в случае реакции ( I), так как в ней принимает участие только один мономер. Поэтому вывод функции распределения будет проведен на примере именно этой, реакции. Если проделать те же выкладки для случая реакции ( II), то получается практически тот же результат. [13]
В нашей работе рассматривается метод расчета и анализа молекулярно-массовых распределений ( ММР) полимеров с учетом длинноцепной и короткоцепной разветвленное, основанный на теории ветвящихся процессов [ 2, с. При выводе функции распределения полимерная молекула представляется в виде диаграммы, которая в теории графов называется деревом, при этом вершины дерева обозначает мономерные звенья в полимерной цепи. [14]
Это поле скоростей соответствует потоку, обладающему градиентом скорости р в направлении у. Нашей целью является вывод функции распределения для стационарного состояния, которая приводит к заданному полю скоростей. Затем будет проведен расчет скалывающего напряжения, необходимого для поддержания течения. Коэффициент - вязкости т ] определяется как напряжение сдвига, приходящееся на единичный градиент скорости в направлении, нормальном к потоку. [15]
Страницы: 1 2