Гипотеза - чаплыгин
Cтраница 2
На этой части передней кромки, с которой сходит [ юсовая нелепа, выполняется гипотеза Чаплыгина - Жуковского о конечности скоростей. Вихревая схема на этой части крыла строится аналогично треугольному крылу. [16]
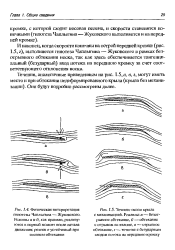 |
Физическая интерпретация гипотезы Чаплыгина - Жукоьекого. Режимы а и fi, как нргшило, реализуются в первым момент после начала / Снижения. режим а устойчивый при плаином обтсклннп. [17] |
И наконец, когда скорости конечны на острой передней кромке ( рис. 1.5, г), выполняется гипотеза Чаплыгина - Жуковского в рамках безотрывного обтекания носка, так как здесь обеспечивается тангенциальный ( безударный) вход потока па переднюю кромку за счет соответствующего отклонения носка. [18]
При безотрывном обтекании решетки профилен отсутствует цепочка носовых пелен ( й ( 0 при всех г), гипотеза Чаплыгина - Жуковского на передних кромках пе используется. [19]
В рассматриваемых задачах необходимо дополнительное условие для определения циркуляции в сечениях несущей поверхности. Таковым обычно является гипотеза Чаплыгина - Жуковского о конечности скоростей на острых задних кромках, что эквивалентно требованию обращения в нуль интенсивности присоединенного вихревого слоя на них. [20]
Возмущенные скорости будем определять сразу от пары вихрей, симметрично расположенных относительно поверхности раздела. Удовлетворяя граничным и начальным условиям и гипотезе Чаплыгина - Жуковского на основном профиле, сведем задачу к решению системы уравнений, из которых находятся циркуляции вихрей, моделирующих основной профиль и его след, но с учетом влияния поверхности раздела. При расчете коэффициентов уравнений, - А также вихревых структур и аэродинамических нагрузок учитываются возмущенные скорости от отображенной вихревой системы. Аналогично проводится расчет тонкого профиля с механизацией. [21]
В этом случае поток плавно огибает передние кромки профиля и закрылка, п которых теоретически получаются бесконечные скорости и разрежения, и затем сходит с задней кромки закрылка по касательной к его поверхности. Обтекание не сопровождается сходом с кромок вихревых поверхностей, и гипотеза Чаплыгина - Жуковского выполняется, как обычно, только па задней кромке закрылка. [22]
Непрерывное решение задачи обтекания в этом случае всегда существует ( при условии М 1) и определяется единственным образом заданием циркуляции скорости по контуру, охватывающему цилиндр. Если контур сечения цилиндра в кормовой части имеет выпуклую угловую точку, то циркуляцию можно определить на основе гипотезы Чаплыгина - Жуковского о сходе линии тока в угловой точке. Доказательство сформулированных утверждений требует глубокого математического анализа. [23]
Устранить эти особенности можно в схеме с безударным входом потока на передние кромки профилей соответствующим отклонением их носков. При этом, как и в случае изолированного профиля, на передних кромках профилей приходится помещать дополнительные контрольные линии, что обеспечивает выполнение здесь гипотезы Чаплыгина - Жуковского. [24]
Гипотеза Чаплыгина достаточно хорошо оправдывается на опыте. По-видимому, это объясняется тем, что если точка схода не совпадает с острием, то вследствие очень больших скоростей вблизи этой точки при сколь угодно малой вязкости образуются вихри, которые и смещают точку схода к острию ( подробнее мы рассмотрим это явление в гл. Следствием гипотезы Чаплыгина является то, что циркуляция Г перестает быть свободным параметром задачи - ее величина определяется по формуле ( 9), если точка 0 е фо известна. [25]
В бесциркуляционных задачах используется требование равенства нуля циркуляции по любому замкнутому контуру, охватывающему любое сечение. Далее будут рассматриваться и такие течения, при которых обеспечивается вход потока на передние кромки несущих поверхностей. Это эквивалентно гипотезе Чаплыгина - Жуковского и на передних кромках, что дает дополнительное условие для определения дополнительных деформаций. [26]
Выбор положения дискретных вихрей и контрольных точек производится аналогично тому, как это делалось на профиле. Суммарные дискретные вихри располагаются на линиях и, ( I ( д п) на расстоянии 1 / 2 длины каждого участка от его начала, а контрольные точки - на линиях v ( I V п - I ш - I) па концах каждого участка. В соответствии с гипотезой Чаплыгина - Жуковского контрольные точки размещаются также па тех кромках тела, с которых сходит нелепа свободных вихрей. Ближайшие к кромкам тела свободные вихри располагаются на конусах, касательных к телу по линии кромок, симметрично по отношению к суммарным вихрям несущей поверхности. При таком принципе схематизации псе контрольные точки оказываются расположенными посередине между соседними дискретными вихрями. [27]
Отметим, что постулировать существование отрывного стационарного режима обтекания в общем случае нельзя, но оно не должно и исключаться. В некоторых случаях нестационарная постановка задач позволяет исправить дефекты стационарного подхода. Примером может служить обтекание симметричного профиля конечной толщины, кормовая часть которого имеет форму клина. Рассмотрение неустановившегося обтекания позволяет корректно выполнить все условия, включая гипотезу Чаплыгина - Жуковского на задней острой кромке, что не удается сделать в стационарном случае. [28]
Рассмотрим отрывное осесимметричиое обтекание кольцевого крыла. В этом случае вихревые поверхности сходят с обеих кромок ( вход ной и выходной) н образуют две системы свободных вихрей - носовую и кормовую. Хорда сечений делится нал равных частей. В результате получается п кольцевых расчетных полос одинаковой ширины. В соответствии с гипотезой Чаплыгина - Жуковского ближайшие к кромкам свободные вихри ( 1 Оир, л 1) размещаются на касательном к кольцевому крылу конусе. [29]
Страницы: 1 2