Передающая апертура

Cтраница 1

Увеличение размеров передающей апертуры также приводит к росту оптимальной мощности и пиковой интенсивности. Для фокусированного пучка при увеличении радиуса пучка вдвое оптимальная мощность передатчика растет линейно, а максимальная плотность мощности на приемнике сильнее, чем по квадратичному закону. [1]

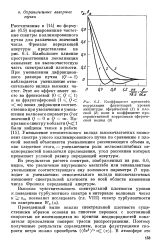Коэффициент временной корреляции флуктуации уровня амплитуды сферической ( 7 и плоской ( 2 волн и коэффициент пространственной корреляции сферической волны ( 3. [2]

Цй ные спектры коллимированного пучка для различных значений ff - числа Френеля передающей апертуры представлены на рис. 6.4. Наибольшее влияние о ц пространственная локализация оказывает на высокочастотную часть спектральной плотности. При уменьшении дифракционного размера пучка ( Q - 1) наблюдается уменьшение относительного вклада высоких частот. Этот же эффект имеет место во френелевой ( 0; Q 1) и во фраунгоферовой ( 1 Q оо) зонах дифракции соответственно при увеличении и уменьшении волнового параметра Q от значений Q О и Q оо. [3]

Характерной особенностью результатов, полученных для обратного распространения, является наличие некоторой высоты передающей апертуры ( Н - 2 кле), при которой наблюдается наибольшее влияние атмосферной турбулентности на расширение пучка. При дальнейшем увеличении высоты, как видно из рис. 4.6, это влияние монотонно уменьшается. [4]

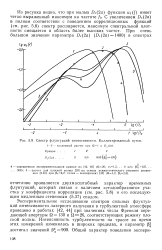Спектр флуктуации интенсивности. Коллимированный пучок. [5]

Экспериментальное исследование спектров сильных флуктуации интенсивности лазерного излучения в турбулентной атмосфере проведено в работах [42, 44] при значениях числа Френеля передающей апертуры Q 130 и Q 26, соответствующих режиму плоской волны. [6]

Дополнительными параметрами, определяющими измеренное распределение вероятностей флуктуации интенсивности лазерных лучков в турбулентной атмосфере, могут быть размер приемной апертуры, условия фокусировки излучения передающей апертурой и, наконец, степень монохроматичности оптического излучения. Влияние всех перечисленных факторов исследовалось экспериментально. Остановимся кратко на полученных при этом результатах. Оказывается, что увеличение размеров апертуры не приводит, как показано в [56, 57], к искажению логарифмически нормального закона. Этот закон сохраняется даже в том случае, когда размер приемной апертуры намного превышает радиус корреляции интенсивности. [7]

Уменьшение относительного вклада высокочастотных компонент спектра узкого коллимированного пучка по сравнению с плоской волной объясняется уменьшением рассеивающего объема и, как следствие этого - уменьшением роли мелкомасштабных не-однородностей показателя преломления, угол рассеяния которых превышает угловой размер передающей апертуры. [8]

Из результатов расчета спектров, изображенных на рис. 6.6, видно, что увеличение внутреннего масштаба или эквивалентное уменьшение соответствующего ему волнового параметра D приводит к уменьшению относительного вклада высокочастотных компонент спектральной плотности во всей области изменения числа Френеля передающей апертуры. [9]

Соотношение между измеренными радиусами пространственной корреляции плоской волны ( Q130), сферической волны ( угол расходимости равен 60) и пространственно ограниченного пучка ( Q l) согласуется с формулой (5.24), определяющей зависимость г / от условий дифракции на передающей апертуре. [10]

Влияние потерь в диэлектрике можно оценить с помощью уравнений (13.67) - (13.70), однако при значениях тангенса угла потерь, меньших 0 001, влияние потерь пренебрежимо мало. Если диаграмму направленности передающей апертуры представить в виде углового спектра и учесть зависимость затухания от углов, то можно сделать вывод, что при малых углах падения волны будут затухать меньше, нежели при больших. Эти эффекты приводят к поправочным членам второго и третьего порядков, которые при затухании, равном 50 дб, приблизительно равны соответственно - 0 9 и - 0 1 дб. [11]

Из формул (5.36) - (5.39) следует, что в условиях сильных флуктуации интенсивности масштаб временной корреляции полностью определяется длиной волны излучения, длиной трассы и интенсивностью турбулентности на трассе. При этом зависимость от дифракционного размера передающей апертуры и фокусировки излучения исчезает. [12]

Основные особенности пространственной структуры флуктуации интенсивности узкого коллимированного пучка, как это видно из результатов, представленных на рис. 6.14, б, качественно остаются такими же, как и в случае сфокусированного пучка. Однако при больших значениях параметра Ds ( 2a) 1 когда эффективный размер пучка определяется не дифракцией на краях передающей апертуры, а его расходимостью за счет турбулентности среды, наблюдается тенденция к уменьшению первого масштаба корреляции. [13]

Количественно оценить возникающую при этом ошибку затруднительно. Однако из физических соображений очевидно, что в случае распространения пространственно-ограниченных пучков интенсивность в точке наблюдения определяется в основном соотношениями между фазами парциальных сферических волн, приходящих из различных точек передающей апертуры. Поэтому можно надеяться, что приближение (6.69) дает удовлетворительную точность при расчетах флуктуации интенсивности. [14]

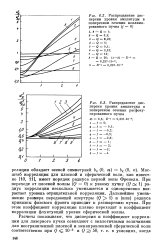Распределение дисперсии уровня амплитуды в поперечном сечении коллими-рованного пучка ( / 0 I, 9 - Q 1. [15]

Страницы: 1 2