Передающая апертура

Cтраница 2

Масштаб корреляции для плоской и сферической волн, как известно [10, 11], имеет порядок радиуса первой зоны Френеля. При переходе от плоской волны ( Q 0) к узкому пучку ( Q - 1) радиус корреляции несколько уменьшается и одновременно возрастает уровень отрицательной корреляции. Дальнейшее уменьшение размера передающей апертуры ( Q 1) и ( или) радиуса кривизны фазового фронта приводит к расширению пучка. При этом коэффициент корреляции плавно переходит в коэффициент корреляции флуктуации уровня сферической волны. [16]

Из рис. 6.12 следует также, что относительная дисперсия в коллимированном пучке увеличивается с ростом значений внутреннего масштаба. Возможно, это увеличение дисперсии связано с блужданиями пучка как целого, которые возрастают с ростом 10 при фиксированном значении Ds. В частности, из физических соображений ясно, что, когда внутренний масштаб превышает размер передающей апертуры / 0 / 2а 1, флуктуации интенсивности будут обусловлены только блужданиями пучка как целого. [17]

Источником служил одномодовый гелий-неоновый ( К 0 6328 мкм) лазер. Максимальный радиус пучка на выходе коллиматора был равен а 6 см. Входное отверстие приемника имело диаметр d 1 мм. На рис. 6.25 показаны измеренные [82] значения относительной дисперсии в зависимости от числа Френеля передающей апертуры. Вертикальные линии соответствуют 99 % - ному доверительному интервалу. [18]

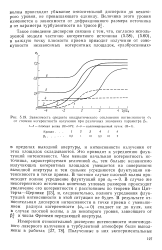Зависимость среднего квадратического отклонения интенсивности а / от степени когерентности излучения при различных значениях параметра РО. [19]

Это приводит к усреднению флуктуации интенсивности. Чем меньше начальная когерентность источника, характеризуемая величиной ак, тем больше независимо излучающих когерентных площадок умещается на поверхности выходной апертуры и тем сильнее усредняются флуктуации интенсивности в точке приема. В частном случае плоской волны происходит полное усреднение флуктуации при ак-0. В случае же некогерентного источника конечных угловых размеров происходит увеличение его когерентности с расстоянием по теореме Ван Цит-терта - Цернике [23], и, следовательно, полного усреднения флуктуации интенсивности в этой ситуации не будет. В результате относительная дисперсия интенсивности в точке приема с уменьшением радиуса когерентности ( aK - Q) спадает не до нуля, как в случае плоской волны, а до некоторого уровня, зависящего от Р и числа Френеля передающей апертуры. [20]

Страницы: 1 2