Современный математический аппарат
Cтраница 1
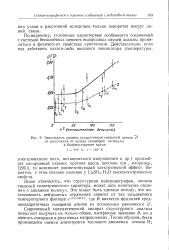 |
Зависимость средних квадратичных смещений атомов и2. [1] |
Современный математический аппарат структурного анализа позволяет получить не только общее, изотропное значение В, но и оценить смещения в различных направлениях. [2]
Использование современного математического аппарата и возможностей вычислительной техники позволяет решать задачи оптимизации рециркуляционных процессов с позиций системного анализа. В связи в этим важное значение приобретает проблема выбора критерия оптимизации. [3]
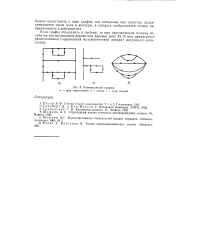 |
Разновидности графов. а - граф гидросистемы. б - дерево. в - граф типовой. [4] |
К ним прилагается разветвленный современный математический аппарат матричного исчисления. [5]
Для более полного представления современного математического аппарата динамики подземных вод приведено изложение основ использования метода интегральных преобразований, получившего широкое применение в специальной литературе. Кроме того, в ряде разделов введены упражнения, проработка которых дает возможность некоторой самостоятельной проверки понимания используемого расчетного аппарата. [6]
В книге представлен важный раздел современного математического аппарата физической химии, основанный на использовании методов линейной алгебры для описания сложных химических превращений. Рассмотрены методы решения наиболее часто встречающихся в физической химии задач, связанных с линейными комбинациями стехиометрических уравнений и с нахождением ряда линейных и степенных функций. Определяются линейные пространства для множеств атомов, молекул, реакций и дается описание мето - - дов расчета термодинамических функций и констант равновесия. Исследуются аддитивные методы расчета физико-химических свойств и проводится их сравнение. Анализируются функции, определенные на молекулярно-стехиометрических уравнениях, и рассматривается теория сложных стационарных реакций. [7]
При решении задач синтеза механизмов широко используется современный математический аппарат теории функций и вычислительной техники. Математические методы пронизывают также изложение разделов анализа механизмов и построения систем управления механизмами машин-автоматов. Поэтому курс теории механизмов и машин по праву относится к механико-математическим дисциплинам. [8]
Электрическая модель дает возможность очень просто с применением современного математического аппарата написать в комплексных переменных уравнение непосредственно для деформации. Однако эта модель, как и предыдущая, не позволяет правильно представить физические процессы, происходящие в материале. [9]
Теоретические основы проектирования машин и линий, базирующиеся на современном математическом аппарате ( теории конечных автоматов, математическом исследовании операций, теории игр и др.), а также на обобщении передового научно-технического опыта, должны обеспечить создание типовых универсальных методов оптимального проектирования, обусловливающих максимальный экономический эффект как на стадиях проектирования и изготовления, так и на стадии эксплуатации оборудования. [10]
В приложении приведены основные понятия, свойства и иллюстрирующие примеры современного математического аппарата анализа и синтеза систем управления. [11]
Математическое описание электромагнитных процессов обычных машин переменного тока составлено с использованием современного математического аппарата через результирующие комплексные функции величин электрических цепей или через их проекции на оси пространственной комплексной плоскости. Запись уравнений и объяснение физических явлений в двух основных разновидностях машин переменного тока ( асинхронных и синхронных машинах) no - возможности унифицированы. [12]
Математическое описание электромагнитных процессов обычных машин переменного тока составлено с использованием современного математического аппарата через результирующие комплексные функции величин электрических цепей или через их проекции на оси пространственной комплексной плоскости. Запись уравнений и объяснение физических явлений в двух основных разновидностях машин переменного тока ( асинхронных и синхронных машинах) no - возможности унифицированы. [13]
Развитие методов оптимизации режимов бурения характеризуется углубленным многофакторным анализом и применением современного математического аппарата. Для практики не потеряли значения и простые методы построения и анализа функций одной или двух переменных типа vM6K f ( P); имах / ( n); uMex / ( f, n) и др. Экстремум функции в случае одной переменной легко найти по стационарной точке. [14]
Математическое описание электромагнитных процессов обычных машин переменного тока составлено с использованием современного математического аппарата через результирующие комплексные функции величин электрических цепей или через их проекции на оси пространственной комплексной плоскости. Запись уравнений и объяснение физических явлений в двух основных разновидностях машин переменного тока ( асинхронных и синхронных машинах) no - возможности унифицированы. [15]
Страницы: 1 2 3 4