Пологая арка

Cтраница 1

Пологие арки ( рис. 78, б) также вытягивают из одного центра. Центр пологой арки располагается ниже, чем в полуциркульной. Доску крепят между откосами и находят центр О. В центр вбивают штырь и с помощью шпагата или рейки определяют места стыкования криволинейной части с прямолинейной. Криволинейную часть арки вытягивают, как у полуциркульной арки. Прямолинейные тяги не доводят до криволинейной на половину длины салазок и затем разделывают линейкой. [1]

Для очень пологих арок это смещение мало разнится от того, которое мы нашли для параболической арки. [2]

Подвеска к фермам и расположение кран-балок. / - кран-балка. 2 - направляющие кран-балок. [3]

При пролетах 30 м и более применяют железобетонные пологие арки, с подъемом / Б-V. Сечение верхнего пояса таких сборных арок обычно двутавровое, затяжку выполняют из предварительно напряженного железобетона. [4]

Параболу часто заменяют дугой окружности, что в пологих арках не приводит к существенному изменению усилий, зато при этом значительно упрощается изготовление и проектирование арок, так как при постоянной кривизне дуги достигается наибольшая стандартизация конструктивных элементов и узлов арки. [5]

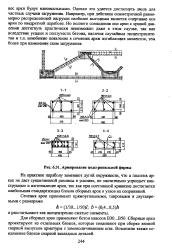Армирование подстропильной фермы. [6]

На практике параболу заменяют дугой окружности, что в пологих арках не дает существенной разницы в усилиях, но значительно упрощает конструкцию и изготовление арки, так как при постоянной кривизне достигается наибольшая стандартизация блоков сборных арок и узлов их сопряжений. [7]

Заметим, что выражение и с плохо поддается вычислению для весьма пологих арок. Для а 18 и а27 третий знак численной величины m и mt уже сомнителен. Эти коэффициенты вычислены с четырьмя знаками для крутых подъемов. [8]

Еще большие трудности возникают при решении задач деформирования таких систем, как пологие арки и пологие оболочки. В частности, как это показано в работе [107], для пологой арки ( рис. В. N имеет вид петлеобразной кривой ( рис. В. [9]

Рассмотрение таблицы XVI показывает, что первое приближение для Я ( для очень пологих арок дает совершенно неудовлетворительные результаты. Второе приближение дает значительные погрешности только для арок сравнительно большой толщины. Влияние нормальной силы и момента на кривизну и на сжатие продольной оси весьма мало и может не приниматься во внимание при расчетах. [10]

Это совпадение объясняется тем, что ординаты круговой оси и параболы в пологих арках мало отличаются друг от друга. [11]

Анализ различных форм непрерывного и дискретного продолжения проведен в [ П5 ] на примере пологой арки и трехстержневой фермы. [12]

График зависимости нагрузки от перемещения в центре для пологой арки, концы которой стянуты пружиной. [13]

На рис. 13 показано более сложное явление типа катастрофы складки, которое может возникать при больших перемещениях пологих арок и куполов. Это явление как при мертвом, так и жестком нагружении недавно исследовалось [ 471 при помощи новой теоремы сопряжения, которая позволяет сделать неочевидные заключения об устойчивости при помощи представления о последовательности складок. На траектории, изображенные на рис. 13, весьма похожи траектории складок для равновесия массивной холодной звезды с двумя устойчивыми режимами, соответствующими белому карлику и нейтронным звездам. Они также изучены ( см. [47]) и будут обсуждаться в следующей главе. [14]

График зависимости нагрузки от перемещения в центре для пологой арки, концы которой стянуты пружиной. [15]

Страницы: 1 2 3 4