Кольцо - фланец
Cтраница 4
Решив уравнения ( 18) относительно Л10, Q0, определяют напряжения в кольце фланца и изгибные напряжения: в основании и вершине конической части втулки. [46]
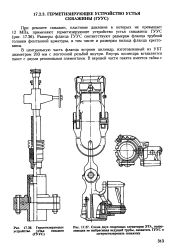 |
Схема двух спаренных элеваторов ЭТА, позволяющих не выбрасывая ведущей трубы, захватить ГУУС и загерметизировать скважину. [47] |
Размеры фланца ГУУС соответствуют размерам фланца трубной головки фонтанной арматуры, в том числе и размерам кольца фланца крестовины. [48]
 |
Наконечник соединения с зажимами для эмалированных сосудов, предложенный И. Г. Шерманом и Л. А. Ярошевской. Штриховая линия - эмалевое покрытие. [49] |
Определенное при этом условии кольцевое напряжение ( 51) есть кольцевое напряжение сжатия на закруглении внутренней грани кольца фланца. Для рассматриваемых сосудов напряжения во фланцах и наконечниках, вызванные изгибной деформацией, и нормальные - изгибным расчетным, не вычисляют ввиду малости этих нормальных напряжений. Погрешность располагается в запас расчета, поскольку знаки изгибного расчетного и нормального к нему напряжения совпадают. [50]
 |
Значение коэффициен та Y. [51] |
Для этого следует при выборе основной расчетной схемы мысленно рассечь оболочку в вершине втулки и при определении перемещений кольца фланца рассматривать его совместно с втулкой. [52]
 |
Случаи нагружения кольцевых пластинок. [53] |
Если учесть малость прогибов кольца по сравнению с его толщиной Ь, то можно показать, что к расчету колец фланцев применима обычно используемая приближенная теория изгиба тонких пластинок. [54]
 |
Расчетная модель сопряжения втулки цельного фланца с кольцом. [55] |
Практическое значение, особенно для фланцев низкого давления, имеет задача о выборе шага болтов, поскольку прогиб w колец фланцев между болтами ( рис. 2, а) может нарушить плотность соединения. В методике эта задача решена на основе рассмотрения деформации дискретно нагруженных пластин. [56]
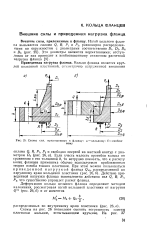 |
Схемы сил, приложенных к фланцу. а - цельному. б - свободному. [57] |
Если учесть малость прогибов кольца по сравнению с его толщиной Ь, то нетрудно показать, что к расчету колец фланцев применима обычно используемая приближенная теория изгиба тонких пластинок. Действие приведенной нагрузки фланца эквивалентно действию сил Q, R, R ], РЗ, что существенно упрощает расчет фланца. [58]
Поскольку в районе прокладки использовалась усовершенствованная, более мелкая сетка конечных элементов, име-ла Сь возможность учесть различные свойства материала колец фланцев и слоев прокладки. [59]
Эта величина га весьма близка к предсказываемой моделью жесткого коль ца, что и объясняет исключительно хорошее совпадение средних поворотов колец фланцев, вычисленных по модели жесткого кольца и по методу конечных элементов. [60]
Страницы: 1 2 3 4 5