Аберрация - система
Cтраница 1
Аберрации системы и конечность размеров источника света ограничивают пределы уменьшения б; поэтому для уменьшения аберраций и, следовательно, уменьшения б в II. [1]
Аберрации системы, полученные из расчета в первом приближении, всегда оказываются довольно большими, и потому прежде всего необходимо выяснить, насколько следует изменить полученные аберрации. [2]
Так как аберрации системы изменяются не скачкообразно, то рассчитать среднюю плотность Р удобно следующим образом. [3]
В работах [96, 189] были исследованы аберрации электронноопти-ческих систем с симметрией вращения при наличии объемных зарядов, причем во второй из указанных работ учтен также релятивистский эффект. [4]
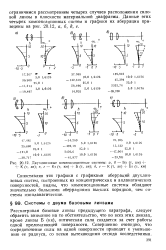 |
Двухлинзовые компенсационные системы. а, б - Бз ( т, км - f. [5] |
Сопоставляя эти графики с графиками аберраций двухлин-зовых систем, построенных из концентрических и апланатических поверхностей, видим, что компенсационные системы обладают значительно большими аберрациями высших порядков, чем системы изопланатические. [6]
Это поле вносит вклад лишь в аберрации системы. [7]
Такой же подход удобен для расчета аберраций систем линз через коэффициенты аберрации отдельных элементов системы. Окончательный вид матриц получается достаточно сложным. Причем в общем случае [151] выражение для любого конкретного коэффициента аберрации системы линз содержит не только соответствующие коэффициенты отдельных линз, а может содержать весь набор их коэффициентов аберраций. Единственным исключением являются аксиальные аберрации, которые зависят только от аксиальных коэффициентов аберраций отдельных линз. Тем не менее смешивание сферической и аксиальной хроматической аберраций также не является простой задачей. Мы вернемся к этому вопросу в разд. [8]
По этой формуле вычисляется в угловой мере меридиональная аберрация системы по, известным значениям поперечных мери-двевальных аберраций в передней фокальной, плоскости как жда ствующей окуляру системы, так и самого окуляра. [9]
Уравнение (5.206) может быть использовано без изменения для вычисления коэффициента аберрации Ссо системы, если рассматривать ее как одну линзу. Эти интегралы появляются в уравнениях (5.310) и (5.311) соответственно. Таким образом, можно выразить коэффициент аберрации составной линзы через коэффициенты аберрации ее компонентов, если учесть, что для составной линзы h ( z) является единственным лучом и h ( zm) h m может принимать любое отрицательное значение. [10]
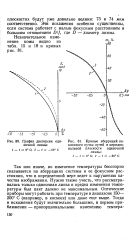 |
График дисторсии одиночной линзы.| Кривые аберраций наклонного пучка лучей в меридиональной плоскости одиночной. [11] |
Так или иначе, но изменение температуры бесспорно сказывается на аберрациях системы и ее фокусном расстоянии, что в определенной мере ведет к нарушению качества изображения. Нужно также учесть, что рассматривалась только одиночная линза и предел изменения температуры был взят далеко не максимальным. Оптические приборы могут работать при температуре в диапазоне 150 - 200 С ( например, в космосе) или даже еще выше. [12]
Перераспределение световой энергии в плоскости изображения зависит, в основном, от аберраций системы и дифракции. Необходимо отметить, что дифракция системы зависит от величины волновых аберраций, определяющих разности хода для всех интерферирующих между собой лучей, а также от формы отверстия, ограничивающего рассматриваемый пучок лучей. Не останавливаясь на конкретном выводе-формул перераспределения световой энергии, зависящей от выше изложенных причин, условимся, что световая энергия распределена в точке А в виде функции Еы на отрезке А. [13]
Если в микроскоп попадает излишний свет, то он может уменьшить контраст изображения вследствие аберраций системы, рассеяния и вредных рефлексов. Во избежание этого полевую диафрагму 3, края которой видны в поле зрения окуляра, открывают лишь настолько, чтобы ее изображение было равно полю зрения. Апертурную диафрагму 4, изображение которой при вынутом окуляре видно в плоскости выходного зрачка объектива 8, обычно открывают так, чтобы ее видимый диаметр был равен 2 / 3 диаметра выходного зрачка. Неполное раскрытие апертурной диафрагмы конденсора несколько снижает разрешающую способность микроскопа, но зато приводит к значительному увеличению контраста изображения. Апертурную диафрагму раскрывают полностью до размера выходного зрачка объектива лишь в тех сравнительно редких случаях, когда требуется реализовать всю разрешающую способность микроскопа. [14]
В случае переноса предмета в бесконечность изображение перейдет в фокальную плоскость составленной системы; при этом аберрации системы соответственно изменятся. [15]
Страницы: 1 2 3