Аберрация - система
Cтраница 2
Вычисление аберраций катодных линз - задача весьма сложная [9], поэтому обычно формой эмитирующей поверхности пренебрегают и считают, что аберрации пушки равны аберрациям системы, формирующей пучок с виртуальным источником. [16]
Расчет этих систем облегчается тем, что достаточно его выполнить для одной точки центра поля; вместе с тем связь радиусов с расстоянием от вершины поверхности до центра симметрии лишает почти полностью эти параметры способности исправлять аберрации системы, н основными, действенными параметрами становятся показатели преломления, но и последние не дают большого простора для изобретательства. Наибольший интерес представляют зеркально-линзовые концентрические системы. [17]
Для реальных оптических систем можно принять разрешающую силу объектива - 30 линий на 1 мм, в таком случае в интерферометрах с полем - 0 100 мм и масштабом изображения - 1: 5 ошибка, вызванная аберрациями системы, составит - 0 15 мм в плоскости исследуемой неоднородности. Учитывая дополнительную потерю за счет зернистости фотоматериала, составляющую 0 05 мм ( для масштаба 1: 5), получим величину общей разрешающей способности - 0 2 мм. Это несколько меньше, чем ошибки, вызванные дифракционными явлениями, но при малых масштабах изображения могут превосходить ее. Следовательно, в отличие от схемы интерферометра Маха-Цендера, где дифракционные ошибки пренебрежимо малы по сравнению с аберрационными [4], для многолучевого интерферометра величины обеих погрешностей соизмеримы. [18]
Такой метод изменения радиусов кривизны и изучение влияния этих изменений на исправление тех или иных аберраций оптической системы были реализованы также и аналитически - путем замены физического изменения кривизны поверхностей отдельных линз тригонометрическим расчетом хода лучей через поверхности разрабатываемой системы и последующего определения изменений аберраций системы. [19]
Однако следует отметить обстоятельство, которое дает возможность, жертвуя небольшой частью световой энергии, добиться хорошей равномерности освещенности плоскости РР1 и стоящих за ней, в частности плоскости экрана ЭЭ Если все светильники одинаковы по форме н стоят на равных расстояниях друг от друга как в вертикальном, так н в горизонтальном направлении, то распределение световой энергии в плоскости PPt носит двоякопериодический характер ( в обоих указанных направлениях); при этом должно соблюдаться условие, чтобы при переходе от одного светильника к следующему аберрации системы LjZ2 оставались постоянными, что всегда происходит, когда число светильников велико. Кроме того, необходимо, чтобы потоки, излучаемые всеми светильниками, были равны. Указанное свойство сохраняетсй и иа плоскости экрана ЭЭt, на котором вследствие размазывания картины распределения освещенности из-за дефокусировки скачки освещенности становятся меньше, чем в плоскости РР, таким образом, возможность уравнять распределение на экране тем же способом, что для плоскости PP-i ( введением рассеивателя), остается н решение задачи облегчается благодаря уменьшению колебаний освещенности. [20]
Члены, не содержащие апертурных углов, определят собой дис-торсию системы. Изучая аберрации кособоких систем, мы ограничимся рассмотрением лишь тех аберраций, которые отсутствуют у центрированных систем; поэтому будем рассматривать лишь аберрации первого и второго порядка - астигматизм, кому и дисторсию. [21]
Практически во многих случаях представляется возможным осуществить разделение падающих и отраженных пучков лучей при сравнительно небольших децентрировках элементов оптической системы. Это обстоятельство может в значительной степени облегчить исправление аберраций нецентрированной системы. [22]
Как волновые, так и геометрические аберрации изменяются с изменением величины апертурных углов при сохранении самой оптической системы неизменной. Поэтому для получения независимых от величин апертурных углов выражений аберраций системы выгодно вводить постоянные коэффициенты аберраций, которые могут охарактеризовать свойства получаемого изображения. [23]
Таким образом, в пятом порядке, как и в третьем, удается выразить аберрации системы через аберрации ее элементов в самом общем виде, однако соответствующие выражения оказываются более громоздкими. По существу, формула (2.22) по сравнению с (2.5) не упрощает аналитического расчета. [24]
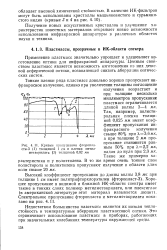 |
Кривые пропускания фторопла-ста-3 ( 1 толщиной 1 см и пленки метилметакрилата ( 2 толщиной 0 02 мм. [25] |
Применение пластмасс значительно упрощает и удешевляет изготовление оптики для инфракрасной аппаратуры. Ценным свойством пластмасс является возможность изготовления из них дешевой асферической оптики, позволяющей снизить аберрации оптичес-ских систем. [26]
Тот же результат можно получить, последовательно преобразуя аберрации от элемента к элементу и каждый раз добавляя искажения, вносимые очередной поверхностью системы. Формула (2.16) математически выражает важный для теории третьего порядка факт: в этом порядке аберрации системы можно выразить в виде суммы аберраций составляющих ее элементов, заданных в их выходных зрачках и пересчитанных в выходной зрачок системы путем соответствующих масштабных изменений зрачковых и полевых координат. [27]
Все светильники должны быть одинаковы, излучать равные потоки и располагаться так, чтобы нх центры н в вертикальном, и в горизонтальном направлении находились на равных расстояниях р и р друг от друга. PPi - Оптическая система ЬгЬг изображает эту плоскость на плоскость Р Р; вследствие аберраций системы L L, этн изображения искажены. Еще больше размыты из-за расфокусировки изображения зрачков в плоскости экрана ЗЭЬ особенно на его краях, но все же колебания освещенности, особенно в середине экрана, где аберрации малы, достаточно велики. [28]
Пятна пересечения луча при входе и выходе из системы не должны налагаться ни на какие другие пятна, соответствующие любому отражению. Для соблюдения этого условия необходимо избегать увеличения диаметра пятна, которое может быть вызвано аберрациями системы или плохим изготовлением поверхности. Расчет показывает, что вследствие малых углов луча с нормалями к поверхности аберрации системы малы. [29]
 |
Оптическая схема укороченного трехлиизового объектива ( Р Ю при Д 0 15. [30] |
Страницы: 1 2 3