Телескопическое кольцо

Cтраница 2

Сопоставление расчетных по уравнению с применением поляризационно-оптического метода ( 1 8 и МК. Э ( 2, 4 и средних экспериментальных величин долговечно-стей для модельного [ 1, 2 ( зона RA. 8, 4 ( зона /. в ] и конструктивного [ 5 ( зона RA ] элементов. [16]

Таким образом, моделирование условий разрушения телескопического кольца показало, что в стендовых испытаниях и в условиях эксплуатации возможны режимы нагружения, когда реализуются разрушения малоциклового характера. На рис. 5.15 приведены также данные расчета малоцикловой усталости модели, полученные с использованием рис. 5.13, 5.14 и табл. 5.2. Соответствие кривых хорошее, лучше при расчете чисел циклов на основе максимальных деформаций в опасных зонах с помощью МК. Здесь же приведены результаты расчета для двух конструктивных элементов 3, испытанных в стендовых условиях по режиму, приведенному на рис. 5.9, г, но со значительным перекосом; разрушение за Л / 1 1672 и ЛГ2 - 2544 циклов приходилось на зону RA - При известной внешней максимальной нагрузке цикла с учетом перекоса и соответствующего анализа определена средняя нагрузка q в локальной зоне перегрузки, е помощью которой на основе данных рис. 5.13 ( точка 5) найдена максимальная деформация, а затем по рис, 5.14 определено расчетное число циклов. [17]

Схематизация режима термомеханического нагружения ( а и процесса циклического деформирования при неизотермическом синфазном ( 6 и изотермическом ( в нагружен. [18]

Таким образом, при моделировании режима нагружения телескопического кольца следует принять изотермическое малоцикловое нагружение с наличием в характерном режиме одного неизотермического термомеханического цикла, обусловленного нагревом и охлаждением детали при выходе на стационарный режим и сбросе тепловой нагрузки. [19]

Для анализа НДС в зонах концентрации напряжений телескопического кольца с учетом его конструктивных особенностей и специфики высокотемпературного нагружения применим расчетно-эксперименталь-ный метод и используем модифицированное соотношение Нейбера (2.106), а также данные о концентрации напряжений в локальных зонах, полученные с помощью поляризационно-оптического метода. [20]

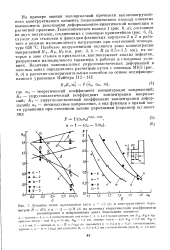Влияние точки приложения силы х - x. l ( a и конструктивных паря-метров R Rlh и т - ( I - х / Н ( б на величину теоретического коэффициента. [23]

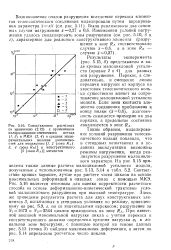
На примере оценки малоцикловой прочности высоконагруженного конструктивного элемента ( телескопического кольца) показана возможность реализации деформационно-кинетической концепции в расчетной практике. Телескопическое кольцо 1 ( рис. 6, а), состоящее из двух полуколец, соединенных с помощью кронштейнов ( рис. 6, б), служит для стыковки и фиксации фланцевых корпусов 2 и 3 и работает в режиме малоциклового нагружения при постоянной температуре 650 С. Наиболее нагруженными являются зоны концентрации напряжений Дд, Л в, RC ( см. рис. 5, Ъ - Л 0 5 - г - 1 5 мм), на которые в зоне стыков и приходятся, как показывает анализ дефектов, разрушения малоциклового характера в рабочих и стендовых условиях. [24]

Таким образом, с помощью моделирования НДС в локальных зонах телескопического кольца выявлена высокая концентрация напряжений на переходных поверхностях радиусами R А и R B и установлено, что высокий уровень концентрации напряжений в этих зонах возникает лишь при крайних положениях точки приложения нагрузки. Существенный вывод следует из анализа зависимости на рис. 3.11: геометрия переходной поверхности радиусом RA не влияет на НДС в опасной точке 3 и теоретический коэффициент концентрации напряжений аа не зависит от этого фактора. [25]

Таким образом, с помощью моделирования НДС в локальных зонах телескопического кольца выявлена высокая концентрация напряжений на переходных поверхностях радиусами RA и Rg и установлено, что высокий уровень концентрации напряжений в этих зонах возникает лишь при крайних положениях точки приложения нагрузки. Существенный вывод следует из анализа зависимости на рис. 3.11: геометрия переходной поверхности радиусом RA не влияет на НДС в опасной точке 3 и теоретический коэффициент концентрации напряжений аа не зависит от этого фактора. [26]

Характер распределения упругих напряжений в зонах возможного разрушения определяем по результатам испытания плоской модели телескопического кольца ( рис. 3.8, а) из оптически активного материала на поляризационно-оптической установке. Плоская модель позволяет достаточно точно воспроизвести НДС в зонах разрушения на концевых участках полукольца. При испытании модели из оптически активного материала имитировали перекос при эксплуатации элементов телескопического соединения путем изменения расстояния JC от точки приложения силы Р до внутренней цилиндрической поверхности кольца и варьировали радиусы R А и R B опасных зон исследуемой детали. [27]

Характер распределения упругих напряжений в зонах возможного разрушения определяем по результатам испытания плоской модели телескопического кольца ( рис. 3.8, а) из оптически активного материала на поляризационно-оптической установке. Плоская модель позволяет достаточно точно воспроизвести НДС в зонах разрушения на концевых участках полукольца. При испытании модели из оптически активного материала имитировали перекос при эксплуатации элементов телескопического соединения путем изменения расстояния х от точки приложения силы Р до внутренней цилиндрической поверхности кольца и варьировали радиусы R А и R B опасных зон исследуемой детали. [28]

Кроме того, при анализе и расчете необходимо учитывать, что предельное состояние локальных зон телескопического кольца формируется в условиях малоцикловой усталости. [29]

Отражены инженерные методы оценки малоцикловой прочности в неизотермических условиях и на примере расчета конструктивного элемента ( телескопическое кольцо) при высокой температуре ( 923 К) показаны способы их реализации. [30]

Страницы: 1 2 3