Волновая аберрация

Cтраница 3

Рассматривая форму кривой волновой аберрации, можно установить, что обычно применяемому исправлению продольной сферической аберрации соответствует не наивыгоднейшее исправление волновой аберрации. [31]

Определим величины остаточных волновых аберраций для случая расфокусировки, соответствующей волновой аберрации для края отверстия, равной нулю. Обозначим волновую аберрацию до расфокусировки через ег, после расфокусировки - через ед. Продольная сферическая аберрация для рассматриваемого случая на краю отверстия была равна нулю. [32]

Такова величина допустимой суммарной волновой аберрации на все оптические детали системы, влияющие на качество ее изображения. [33]

Определим уравнение кривой нулевой волновой аберрации. [34]

При исследовании малых и неоднородных волновых аберраций преимущество имеет метод получения интерферограмм на фоне полос конечной ширины, которые образуются при наклоне на некоторый угол е плоскости фронта опорного пучка относительно плоскости фронта измерительного. Схема интерферирующих полей при сведении пучков под углом е показана на рис. 4.2 а. Здесь ( как и на рис. 4.1, а) плоские волновые фронты представлены расположенными на расстоянии А, прямыми линиями, соответствующими определенной фазе колебаний; пересечения фронтов соответствуют максимумам интерференционной картины. Поскольку оба пучка распространяются с одинаковой скоростью вдоль направлений АИ и АО, система полос будет двигаться вправо вдоль биссектрисы угла ОАИ. [35]

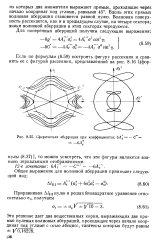Сферическая аберрация при коэффициентах 6A t - С. [36]

Вдоль этих прямых волновая аберрация становится равной нулю. Волновая поверхность рассекается, как и в предыдущем случае, на четыре сектора; знаки волновой аберрации в этих секторах чередуются. [37]

Сами по себе волновые аберрации от отдельных элементов системы при их переносе через какую-либо часть системы сохраняются неизменными; поэтому в случае суммирования при наличии промежуточной дисторсии происходит рассогласование 9.1. К суммированию аберраций апертурных углов. [38]

В этом случае волновые аберрации для обоих волновых фронтов равны нулю ( фиг. [39]

Фигура кружка рассеяния для объектива Руссар-63.| Сферическая аберрация при коэффициентах. [40]

Вдоль этих прямых волновая аберрация становится равной нулю. [41]

Таким образом, волновые аберрации сферической волны, падающей на оптический элемент, если они вычислены на поверхности элемента, должны быть просто сложены с аберрациями, которые вносит этот элемент, когда на него падает идеальная сферическая волна. [42]

Рассмотрим картину изменения волновых аберраций на различных участках зрачка системы. [43]

Рассматривая же изменение волновой аберрации вдоль оси ut, увидим, что в этом случае волновая аберрация изменяется по квадратичному закону. [44]

Рассмотрим картину изменения волновых аберраций на различных участках зрачка системы. [45]

Страницы: 1 2 3 4