Сферическая аберрация - третье
Cтраница 1
Сферическая аберрация третьего, пятого и даже седьмого порядков встречается довольно часто. В более или менее широкоугольных оптических системах, в пучках, оси которых составляют большие углы с осью системы, а апертурные углы в самих наклонных пучках невелики, можно с успехом ограничиваться определением аберраций третьего порядка; наоборот, на оси системы, где апертурные углы принимают большие значения, необходимо учитывать сферическую аберрацию пятого, а иногда и еще более высокого порядка. [1]
Дополнительно к сферической аберрации третьего и пятого порядков можно добавить также расфокусировку А, которую можно рассматривать как аберрацию первого порядка. [2]
Наиболее важной представляется сферическая аберрация третьего порядка. [3]
Предложение XXXI дает формулу для поперечной сферической аберрации третьего порядка для частного случая, когда луч падает параллельно оси. Ньютон указывает, что им выведена и формула для общего случая, когда предмет находится на конечном расстоянии, но она не приводится. [4]
Для всех шести случаев определим также сферическую аберрацию третьего порядка с тем, чтобы иметь возможность суждения о порядке граничных величин расхождения между реальной сферической аберрацией и сферической аберрацией третьего порядка. [5]
Одним из наиболее характерных случаев подобного рода является сочетание сферической аберрации третьего и пятого порядков, часто встречающееся при образовании изображения точки на оси системы. Целесообразность такого сочетания объясняется тем, что для осевого пучка лучей имеют место наибольшие апертур-ные углы и для их уменьшения невозможно прибегнуть к геометрическому виньетированию. [6]
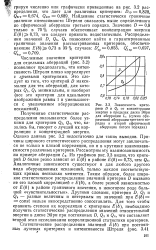 |
Зависимость критериев D и С. 4 от концентрации энергии в пределах диска Эйри для аберрации L4 ( сумма сферической аберрации третьего порядка и второй сферической аберрации пятого порядка. [7] |
Найденное статистически граничное значение интенсивности Штреля оказалось выше определенного по сферической аберрации третьего порядка. [8]
В этом случае наблюдается наибольшее расхождение между действительной сферической аберрацией и сферической аберрацией третьего порядка. [9]
В этом случае наблюдается наибольшее расхождение между действительной сферической аберрацией и сферической аберрацией третьего порядка. [10]
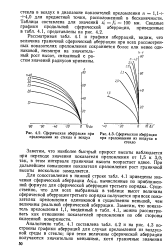 |
Сферическая аберрация при [ IMAGE ] Сферическая аберрация преломлении из стекла в воздух при преломлении из воздуха в. [11] |
Для сопоставления в нижней строке табл. 4.1 приведены значения сферической аберрации Asni, вычисленные по приближенной формуле для сферической аберрации третьего порядка. Существенно, что для всех выбранных в таблице высот величина сферической аберрации третьего порядка получается при всех показателях преломления одинаковой и существенно меньшей, чем величины реальной сферической аберрации. Заметим, что показатель преломления 1 1, введенный в табл. 4.1, можно рассматривать как отношение показателей преломления по обе стороны склеенной поверхности. [12]
На оси системы при более или менее значительных апертурных углах нередко приходится иметь дело со сферической аберрацией пятого порядка, более высокого, нежели сферическая аберрация третьего порядка. [13]
Чтобы установить граничные значения этих критериев, гарантирующие высокое качество изображения, можно было бы опять воспользоваться как эталоном установившейся оценкой качества изображения для сферической аберрации третьего порядка, но такой подход не обеспечивает достоверности оценки при других видах искажений. [14]
Для всех шести случаев определим также сферическую аберрацию третьего порядка с тем, чтобы иметь возможность суждения о порядке граничных величин расхождения между реальной сферической аберрацией и сферической аберрацией третьего порядка. [15]
Страницы: 1 2