Вычислительный аспект

Cтраница 1

Вычислительные аспекты обоих алгоритмов интегрирования идентичны. [1]

Вычислительный аспект моделирования состоит в разработке и реализации так называемого моделирующего алгоритма. [2]

Вычислительные аспекты процессов идентификации, описанных выше, связаны с решением конкретных задач и касаются точности вычислений, скорости сходимости оценок параметров к их истинным значениям, временных характеристик запросов на цикл идентификации. [3]

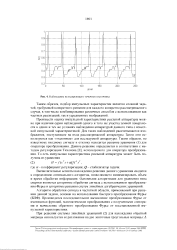Наблюдение пульсирующего точечного источника. [4]

Вычислительные аспекты нахождения решения данного уравнения сводятся к определению оптимального алгоритма, позволяющего минимизировать объем и время обработки информации. Основными алгоритмами для уравнения типа свертки являются алгоритмы обработки сигнала с использованием преобразования Фурье и алгоритмы решения систем линейных алгебраических уравнений. [5]

Подробно вычислительные аспекты твердотельного представления объектов описаны в § 3.2. Можно выделить [125] следующие преимущества этого подхода: концептуальная простота, малый объем требуемой памяти, принципиальная застрахованность от создания противоречивых конструкций, приспособленность к усложнению модели, относительная простота представления частей и сечений общей сцены. К недостаткам обычно относят следующие: метод построения объекта ограничен рамками булевых операций, метод требует вычислительноемких алгоритмов обработки, невозможность использования параметрически описанных поверхностей, которые не позволяют устанавливать положение полупространства, сложности создания и обработки объектов, поверхность которых описана функциями более чем второй степени. [6]

Важным вычислительным аспектом алгоритма является то, что на каждой итерации находится допустимое решение исходной задачи с невозрастающей целевой функцией. Таким образом, вычисления могут быть закончены в любой точке с получением решения, в котором целевая функция не выше, чем во всех предшествующих точках. [7]

Рассмотрим вычислительные аспекты метода главных компонент. [8]

Рассматривая вычислительные аспекты решения задач на основе модели МОБ, отметим, что основной объем расчетов связан с вычислением матрицы коэффициентов полных материальных затрат В. Если матрица коэффициентов прямых материальных затрат А задана и является продуктивной, то матрицу В можно находить либо по формулам прямого обращения матриц, либо с использованием итерационных методов. [9]

Рассмотрим вычислительные аспекты решения задачи ( 111 - 40) - ( 111 - 41), которую ниже будем называть исходной. [10]

Приводятся наиболее важные теоретические и вычислительные аспекты метода граничных интегральных уравнений; в качестве иллюстративного примера рассматривается решение задач для уравнения Лапласа. [11]

Касаясь вычислительного аспекта предлагаемого метода, отметим, что полученные уравнения в принципе решаются стандартными программами с наперед заданной точностью. Однако поскольку в решении задачи Б имеет значение лишь конечная точка траектории, то здесь рационально использовать более грубые методы, которые могут дать выигрыш во времени на порядок и более без заметной потери точности конечного результата. Эта рационализация особенно целесообразна в данном случае, поскольку уход от точной траектории легко контролируется по точности выполнения на траектории равенств, дифференцированием которых получены соответствующие дифференциальные уравнения. [12]

Рассмотрены также вычислительные аспекты теории систем, связанные с численными методами решения задач, возникающих на практике. [13]

Имеется несколько других вычислительных аспектов эффективного применения методов из разд. Очевидно, что, когда набор исходных данных требуется использовать неоднократно, хранение этого набора в памяти приводит к меньшей затрате машинного времени по сравнению с тем случаем, когда каждый раз приходится восстанавливать этот набор. Для небольших задач это осуществимо, однако для больших задач требуемый объем памяти может легко превысить возможности мощных компьютеров. Поэтому необходимо хранить в памяти только часто используемую информацию. Матрицы коэффициентов уравнения состояния (4.43) и сопряженного уравнения (3.32) для данного условия повреждения совпадают. [14]

Дисперсионный анализ в вычислительном аспекте основан на разложении дисперсии Сто на составляющие, порождаемые независимыми факторами. [15]

Страницы: 1 2 3 4