Система ах
Cтраница 2
Пусть в системе Ах Ъ возмущается только вектор Ь, т.е. вместо исходной системы решается возмущенная система Ах b b ( b, и пусть х - точное решение возмущенной системы. [16]
Для того чтобы система Ах b имела решение, необходимо и достаточно, чтобы гиперповерхность (91.2) имела центр симметрии. Множество всех решений совпадает с множеством всех центров симметрии. [17]
Образуют ли решения системы Ах 0 конус. [18]
А, то решение системы Ах - Ь легко найти. [19]
Каждый столбец матрицы А из системы Ах b есть вектор с т компонентами. [20]
А не равно нулю, то система Ах у, x г разрешима. [21]
В этом случае говорят, что система Ах Ь несовместна. [22]
К этому всегда можно прийти, исключив из системы Ах Ъ линейно зависимые уравнения. [23]
Дополнительно к основной системе Oxyz с кривошипом связана вспомогательная система Ах у, в которой Ау есть ось вращения кривошипа /, ось Azi параллельна оси Ог и ось Axl перпендикулярна к осям Лг / г и Агг и образует с ними правую систему. Кривошип / вращается в плоскости Ах, и его положение определяется углом аи. [24]
Если ранг матрицы А равен г, то однородная система Ах - - 9 имеет п - г линейно независимых решений, а однородная система A g 9 имеет т - г таких решений. [25]
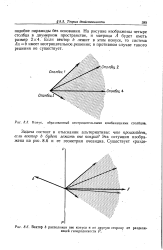 |
Конус, образованный неотрицательными комбинациями столбцов.| Вектор Ь расположен вне конуса и по другую сторону от разделяющей гиперплоскости Р. [26] |
Если вектор b лежит в этом конусе, то система Ах Ь имеет неотрицательноефешение; в противном случае такого решения не существует. [27]
Пусть л: ( лг -) ( удовлетворяет системе Ах Ь и rf ( afj) представляет собой агарэвлеН Не, выработанное этим методам. [28]
Выбор осуществляется по следующему правилу: оптимальным среди всех решений системы Ах - р является решение с минимальной длиной. Это означает, что любой вектор может быть разложен на две перпендикулярные составляющие - проекцию на пространство строк и проекцию на нуль-пространство. Тогда л: х, - f - w, где хг принадлежит пространству строк, a w - нуль-пространству. [29]
Лица, изучающие линейную алгебру, узнают также, что решение системы Ах - Ь можно представить в виде хА - 1Ь, где А 1 - матрица, обратная для А. [30]
Страницы: 1 2 3 4