Математик

Cтраница 1

Математик может доказать что-либо только относительно математического объекта, а кусок веревки - это объект физический. Поэтому прежде, чем думать о доказательствах, мы должны позаботиться о математическом определении узла и того, когда два узла должны рассматриваться как одинаковые. Подобная проблема построения математической модели возникает всякий раз, когда математику применяют к некоторой физической ситуации. [1]

Математик должен принять во внимание образование и психологию людей, применяющих разработанные им методы и программы. Например, простейшая программа численного интегрирования, предназначенная для широкого круга нематематиков, использующих ЭВМ в своих конкретных исследованиях, должна быть рассчитана на человека, потолок математических знаний которого находится на интуитивном понимании того, что интеграл - это площадь. Чтобы не затруднять пользователя, в описании простейших программ даже ничего не говорится о точности результата. [2]

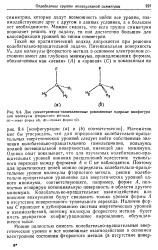Две симметрически-эквивалентные равновесные ядерные конфигура. [3]

Математик мог бы утверждать, что для определения колебательно-вращательных энергетических уровней следует найти собственные значения колебательно-вращательного гамильтониана, пользуясь полной потенциальной поверхностью, имеющей два минимума. Однако опыт показывает, что для изучаемых колебательно-вращательных уровней никаких расщеплений вследствие туннельного перехода между формами Л и С не наблюдается. Поэтому для практических целей можно определить колебательно-вращательные уровни молекулы фтористого метила, решив колебательно-вращательное уравнение для энергетических уровней одного минимума, соответствующего, например, форме А, полностью игнорируя потенциальную поверхность в области другого минимума. [4]

Математик заметил бы, что все эти рассуждения все еще применимы, когда алгебра определяется над любым полем. Есть поля, которые обладают тем свойством, что в них умножение определенного целого числа, скажем, А, на любое число из поля дает нуль; мы можем сказать, что h аннулирует любое число. Такие модулярные поля надо исключить, поскольку мы хотим сохранить возможность нахождения такого числа, произведение которого с h есть любое заданное число. Когда наши рассуждения не вовлекают никаких других ограничивающих предположений о поле чисел, мы оперируем в относительно элементарной области теории. [5]

Математик Риман ( Riemann) был первым, кто попытался понять механизм передачи звука в среднем ухе, состоящем из барабанной перепонки и системы косточек. Риман рассматривал среднее ухо как нечто целое и полагал, что звуковые колебания распространяются в ухе, как они распростра-няются в твердом теле. С этой точки зрения был непонятен смысл сложной структуры среднего уха. Гельмгольц, изучив анатомию среднего уха, пришел к убеждению, что в системе, состоящей из барабанной перепонки и косточек, передача колебаний происходит совершенно иным способом, и барабанная перепонка Т ( фиг. [6]

Математик любит прежде всего симметрию. [7]

Математик не может без негодования смотреть, как физик суммирует бесконечные ряды, предполагая при этом, что два-три члена ряда дают хорошее приближение ко всему ряду, и вообще живет в царстве свободы, нарушая все моральные нормы. [8]

Математик, даже если он занимается прикладными задачами, пришедшими не из математики, берется за решение только тех проблем, которые не требуют дополнительных недосказанных предположений. Физик, как правило, имеет дело с задачами, в которых имеющихся исходных данных недостаточно для решения, и искусство состоит в том, чтобы угадать, какие недостающие соотношения реализуются в природе. Именно для этих догадок требуется не математическая, а физическая интуиция. [9]

Математик видит в моделировании на вычислительных машинах рабочий инструмент для решения задач математической логики и задач вычислительного характера. Для него это всего лишь одно из нескольких находящихся в его распоряжении средств получения решения, которое он применяет в наиболее подходящих случаях. Математическое моделирование для него так же старо, как самое математика, а современным является только использование электронных вычислительных машин. [10]

Математик из Университета Монаш в Австралии Джон Стиллуэлл предлагает следующую задачу. [11]

Математик не имеет преимуществ при выборе этой гипотезы; но как только гипотеза выбрана, он должен внимательно следить, чтобы не принять другую, ей противоречащую. [12]

Математик, желающий консультировать инженеров, должен поэтому изучать не только те задачи, которые уже встречались; он также должен быть готов анализировать задачи, которые только еще могут возникнуть. Можно считать, что практические задачи образуют в известном смысле определенный тип задач. Например, очень часто практическая задача принимает форму дифференциального уравнения. Некоторые дифференциальные уравнения мы умеем решать, а другие нет. Поэтому математик стремится расширить свой арсенал, изучая те дифференциальные уравнения, которые пока еще не решены; это неизбежно поставит перед ним ряд фундаментальных вопросов, например. Какая разница между уже решенными и нерешенными дифференциальными уравнениями В чем состоит трудность их решения. [13]

Математик возразил, что для двух таких диаграмм Венна можно образовать пересечение и объединение, а потому они не являются различными видами. Она согласилась, но все же спросила: А зачем тогда овалы вокруг диаграмм Венна. [14]

Математик, механнк и физик; уроженец Швейцарии; член Петербургской ( 1727 - 1783) и Берлинской ( 1741 - 1766) АН. [15]

Страницы: 1 2 3 4