Математика - веко
Cтраница 2
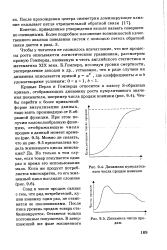 |
Динамика кумулятивного числа продаж новинки.| Динамика числа продаж. [16] |
Чтобы у читателя не сложилось впечатление, что все процессы роста описываются логистическим уравнением, рассмотрим кривую Гомперца, названную в честь английского статистика и математика XIX века. [17]
Шлезингер, высказывая мысль, что Эйлер пришел бы к количественному методу, если бы он поставил задачу действительно определить величину допущенной погрешности, говорит, что история математики еще должна осветить вопрос, почему математики XVIII века и в их числе такие, как Эйлер и Лагранж, не пошли по пути, который спустя несколько десятилетий проложили Гаусс, Больцано, Коши и Абель. На этот вопрос мы сделали попытку ответить во вступительном слове к Дифференциальному исчислению Эйлера 2); мы полагаем, что высказанные там соображения применимы в полной мере и к Интегральному исчислению Эйлера. [18]
Фактически оно должно было бы основываться на доказательстве существования корня любого алгебраического уравнения с действительными коэффициентами: для такого доказательства ( исключая простейший случай уравнения нечетной степени или уравнения ЧЕТНОЙ степени с отрицательным свободным членом) математика XVIII века еще не создала почвы. [19]
Согласно теореме единственности голоморфная функция полностью определяется ее значениями в сколь угодно малой окрестности какой-либо одной точки. Многие математики XVIII века были весьма искусны в аналитическом продолжении. [20]
Есть сходство между английской математикой восемнадцатого века и античной математикой позднеалексаыдрийской эпохи. В обоих случаях неподходящие обозначения технически затрудняли прогресс, а причины того, что математики ими удовлетворялись, были более глубокого общественного характера. Ведущим английским, вернее пользовавшимся английским языком, математиком этого периода был Колин Маклорен, профессор Эдинбургского университета, последователь Ньютона, с которым он был лично знаком. Его исследования н обобщения флюксионного метода, работы по кривым второго и более высокого порядка л по притяжению эллипсоидов шли параллельно с исследованиями Клеро и Эйлера. Некоторые из теорем Маклорена вошли в нашу теорию плоских кривых и в нашу проективную геометрию. [21]
Иногда шутя он мне говорил: Мы-то с Вами знаем, что математика XX века - это и есть теоретическая физика. В то время я разделял эту точку зрения, однако спустя два десятилетия после Ландау методы современной математики - топология, алгебраическая геометрия, теория множеств - проникли в современную физику и эффективно используются при решении физических задач. [22]
Что такая общая теория полей возникла тогда, когда был накоплен, в более частных исследованиях, соответствующий конкретный материал, показывает сноска Штейница к процитированному месту: К этим общим исследованиям особым стимулом для меня была Теория алгебраических чисел Гензеля1), исходным в которой является поле р-адических чисел - поле, которое нельзя отнести ни к функциональным, н к числовым полям в обычном смысле этих терминов. Так новая алгебра ( абстрактная алгебра) естественно вырастала из теоретико-числовых и арифметических исследований, составлявших одно из главных направлении в математике XIX века и уходящих своими корнями в ту наивную проблему решения алгебраических уравнений, с многовековой историей которой читатель уже знаком. [23]
Существуют, однако, несколько иные обстоятельства, также вызывающие необходимость характерной терминологии, при которой опять вводятся в употребление слова чистый и практический без надлежащего оправдания. В своем фундаментальном трактате о круге Архимед открыл, что длина окружности не только не может быть точно вычислена, но даже не может быть определена точно. Точные алгебраические методы были поэтому заменены другого рода подходом, который греки назвали методом исчерпывания; математики XIX века приняли название метода пределов. Применяя этот метод пределов, часто приводящий к разложению в бесконечный ряд, мы стремимся не получить искомую величину, а только приблизиться к ней с ошибкой, которая может быть сделана сколько угодно малой. [24]
Гораздо поучительнее видеть, как ясные, логичные идеи постепенно вырисовываются из беспорядочного нагромождения понятий, чем просто начинать с изложения этих идей. Если четко объяснить, в каких пределах применимы старые методы, то, мне думается, не так уж много вещей придется переучивать. Не знаю, сочтут ли необходимым математики будущих веков говорить о так называемых доказательствах, принятых математиками XX века - возможно, что да. [25]
Уравнения в частных производных, с которыми имеет дело математическая физика, можно рассматривать как их обобщение на бесконечномерные фазовые пространства. Это требует перехода от математического анализа, с которым имели дело Ньютон и Лейбниц, к функциональному, ставшему важным инструментом математики XX века. Согласно традициям, сложившимся в XVIII-XIX веках, основным типом математической модели в физике являлись дифференциальные уравнения, описывающие некую реально Существующую систему. Эти уравнения необходимо составить, исходя из законов физики, а затем найти их решение. [26]
Настоящая монография представляет собой уникальный труд, отличающийся, во многих отношениях, от известных книг по математической физике. Их авторы обычно ограничивались традиционными методами математической физики. Тирринг приводит новые мощные методы: дифференциально-геометрические и операторно-алгебраические, будучи убежденным в том, что было бы нелепо, если бы будущие физики XXI века изучали математику XIX века. [27]
Преследуя в основном чисто логические цели, эта теория была мало приспособлена для вычислений и алгебраических построений. Современные теории ведут начало скорее от работ Гаусса ( 1812), Больцано ( 1817), в особенности от знаменитого Курса алгебраического анализа Коши ( 1821), где в качестве основания, считающегося очевидным, был принят принцип вложенных отрезков. Таким образом, определение системы вещественных чисел было приведено к определению системы рациональных чисел и тем самым к определению системы натуральных чисел. Гильбертом ( 1900) он был включен в число основных проблем математики XX века. Гильберт указал и допустимые ( финитные) средства для такого доказательства; однако Гедель ( 1931) показал, что этими средствами проблема в принципе не может быть решена. С законностью применения таких средств далеко не все математики согласны. [28]
Математика развивается по восходящей линии, минуя все заторы, ее развитие схоже с развитием живого организма. К тому же в математике несравненно явственней, чем в других дисциплинах ощущается, насколько растянуто шествие всего человечества. Среди наших современников есть люди, чьи познания в математике относятся к эпохе более древней, чем египетские пирамиды, и они составляют значительное большинство. Математические познания незначительной части людей дошли до эпохи средних веков, а уровня математики XVIII века не достигает и один человек на тысячу. Но расстояние между теми, кто идет в авангарде, и необозримой массой путников все возрастает, процессия растягивается и идущие впереди отдаляются все более и более. Они скрываются из виду, их мало кто знает, о них рассказывают удивительнейшие истории. Находятся и такие, кто просто не верит в их существование. [29]
Иметь надежную общую основу для многочисленных математических дисциплин нужно было не только для их сведения в единую систему, но п для решения многих проблем, например в теории множеств и теории функций. Наряду с многими конкретно поставленными вопросами ( примером последних может служить вошедшая в знаменитый список Гильберта ( седьмая) проблема определения арифметической природы чисел вида as, когда a - алгебраическое число1), ji - алгебраическая иррациональность) девятнадцатый век завещал своему преемнику немало проблем, имевших первостепенное значение для развития отдельных математических дисциплин. Таковы многие проблемы Гильберта, таковы, например, проблема собственных значений и собственных функций в классических краевых задачах математической физики ( она проходит через все девятнадцатое столетие) п проблема малых знаменателей в небесной механике, восходящая еще к восемнадцатому веку. Именно такая переходная тематика в значительной мере определяла направление исследований в те пятнадцать - двадцать лет, которые образуют первый перпод в истории математики XX века. [30]
Страницы: 1 2 3