Матрица - плотность
Cтраница 1
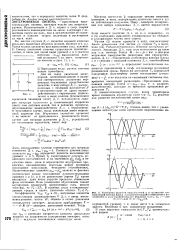 |
Колебания разности населенностей ги и активной составляющей вектора Блоха v ( соответствующей коэффициенту поглощения Е ноле прямоугольного импульса T TI, Ts. I -для 6 0. 2-для 6n 2dbaA / fc. [1] |
Матрица плотности р определяет отклик вещества ( электрич. [2]
Матрица плотности, матрица рассеяния и другие О. [3]
Матрица плотности (2.12) играет роль, аналогичную функции распределения в статистической физике. [4]
Матрица плотности (27.15) описывает свободную прецессию спинов после выключения переменного поля. [5]
Матрица плотности у обладает свойствами проекционного оператора, проецирующего произвольную функцию ( определенную в пространстве спин-орбиталей К) на пространство занятых спин-орбиталей. [6]
Матрица плотности (1.56) зависит только от переменных динамической системы; для диссипатив-ной системы при этом принимаются усредненные по ансамблю значения, вследствие чего флуктуации системы остаются неучтенными. В действительности же диссипативная система стохастическим образом влияет на динамическую систему, так что наряду с затуханием ( релаксация) возникают флуктуации. [7]
Матрицы плотности систематически рассматриваются в разд. [8]
Матрица плотности pj имеет диагональный вид, так что молекулярные орбитали фг и Kt и любые другие орбитали, полученные из них путем унитарных преобразований, будут естественными спин-орбиталями. [9]
Матрица плотности р4 имеет диагональный вид, так что молекулярные орбитали ф, и; и любые другие орбитали, полученные из них путем унитарных преобразований, будут естественными спин-орбиталями. [10]
Матрица плотности обладает свойствами проекционного оператора, проецирующего произвольную функцию ( определенную в пространстве спин-орбиталей X) на пространство занятых спин-орбиталей. [11]
Матрица плотности дает возможность одновременно вычислять квантовомеханические матричные элементы и средние по статистическому ансамблю. Она находит все возрастающее применение в задачах статистической механики. [12]
Матрица плотности похожа на корреляционную функцию для случайного набора классических волн. [13]
Матрица плотности р в этом так называемом смешанном случае ( определенная волновая функция отсутствует) менее ограничена. Например, р12 может обращаться в нуль, в то. [14]
Матрица плотности р представляет собой метод наиболее общего описания любой квантовой системы. Диагональные элементы р, pmm описывают заселенности состояний, а неднагональные элементы р т, pmn - корреляцию между этими состояниями. Величина g pmn / ( pnnpmm) явлется мерой когерентности системы. [15]
Страницы: 1 2 3 4