Матрица - линейная система
Cтраница 1
Матрица линейной системы ( 70) отличается от матрицы А по структуре мало - только добавлением одного ненулевого столбца. [1]
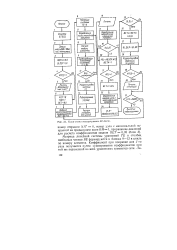 |
Блок-схема подпрограммы SCALCU. [2] |
Матрица линейной системы уравнений ТЕ и столбец свободных членов BE формируются в блоках 9 - 12 в цикле по номеру элемента. Коэффициент при поправке для J - ro узла получается путем суммирования коэффициентов при той же переменной во всех уравнениях элементов сети. [3]
Для численного решения системы ( 6) использовалась схема 4 из § 1.2. Матрица линейной системы для определения множителей Лагранжа здесь трехдиагональная. [4]
Однако определенный интерес представляет развиваемый ниже подход, связанный с исследованием чувствительности собственных значений матриц линейных систем. [5]
Всегда ли возможна схема преобразований (1.46) или, другими словами, всегда ли число нулевых начальных параметров матрицы X линейной системы будет равно числу независимых конечных параметров матрицы У. [6]
Заметим, что такое приведение возможно и в случае равных частот со, 0, но при этом элементарные делители определяющей матрицы линейной системы должны быть простыми. [7]
Под модальным управлением понимают ту часть теории линейных систем, в которой изучаются вопросы синтеза линейных преобразований состояния во вход либо синтеза линейных систем, преобразующих выход линейных систем во вход, которые обеспечивают заданное расположение в комплексной плоскости собственных значений, соответствующих матрице линейной системы. Методы синтеза таких представлений основаны на особой форме минимальных представлений системы, которая называется канонической формой. [8]
На каждом слое схема ( 19) представляет собой систему линейных уравнений для определения величин г; правые части этих уравнений известны, поскольку содержат значения решения с предыдущего слоя. Матрица линейной системы трехдиагональна, и решение можно вычислить алгебраической прогонкой. [9]
Получивший в последнее время интенсивное развитие метод конечных элементов свободен от ряда недостатков описанных методов: он не требует специальных усилий по построению системы базисных функций, являющейся сильно минимальной, при его использовании упрощается написание уравнений вблизи границы. Матрица линейной системы уравнений содержит относительно малое число ненулевых элементов. [10]
Локальные матрица и вектор-столбец. Для формирования матрицы линейной системы разностных уравнений удобно записать полученные выше соотношения для частных производных функционала л-го элемента в матричном виде. Для получения матричной записи принято использовать так называемую локальную нумерацию узлов и соответствующих им неизвестных температур, действующую только в рамках каждого конкретного элемента разбиения. [11]
Напишите фортран-программу, которая использует подпрограммы DECOMP и SOLVE для нахождения усилий из этой линейной системы уравнений. Xopoftio ли обусловлена матрица линейной системы. [12]
При введении нумерации узлов желательно, чтобы максимальная разность их номеров для каждого элемента была минимальной. Это улучшает обусловленность матрицы линейной системы, так как большие коэффициенты оказываются ближе к главной диагонали. [13]
В принципе, уравнения движения и схема метода для этой задачи в трехмерном случае ничем не отличаются от уравнений ( 1) - ( 3) § 7.1. Однако, с точки зрения реальных вычислений, выбор базисных функций здесь очень существенен. Описанный в § 7.1 алгоритм вычисления матрицы линейной системы ( 8) ( скалярных произведений ( 9)) содержит порядка Nm2 / 2 операций, где N - общее число частиц, а га - число базисных функций, пересечение носителей которых содержит данную частицу. В результате, число операций при вычислении матрицы увеличивается на два порядка. [14]
В данной работе мы предлагаем метод проверки идентифицируемости, позволяющий несколько уменьшить сложность символьных выражений. Уравнения, полученные с помощью метода преобразования подобия, являются билинейными, мы же рассматриваем их как линейные относительно части неизвестных. На первом этапе матрица линейной системы уравнений перестановками строк и столбцов приводится к верхнему блочно-треугольному виду. Затем, применяя метод Гаусса отдельно к каждому диагональному блоку матрицы, на основании условия совместности системы линейных уравнений мы генерируем результирующие системы нелинейных уравнений, которые проверяем на разрешимость с помощью метода базисов Гребнера. [15]
Страницы: 1 2