Матрица - гамильтониан
Cтраница 1
Матрица гамильтониана имеет квадратную форму и вследствие равенства Я2з 32 ( а в общем случае Ны /) симметрична относительно главной диагонали. [1]
Матрица гамильтониана может быть построена для любой спиновой системы с использованием базисной функции fk на основании простых формул. [2]
Матрица гамильтониана системы трех спинов имеет порядок 8 - пр числу базисных функций и стационарных состояний. Гамильтониан совокупности ядер Н содержит только диагональные элементы; все недиагональные элементы равны нулю. [3]
 |
Изображение Sd-орбиталей, показывающее расположение лепестков орбиталей относительно осей х, у к г. [4] |
Матрицу гамильтониана для иона в - состоянии в октаэдрическом поле можно получить тем же методом, что и для иона в Р - состоянии. Они могут быть рассчитаны с помощью соотношений ( Б-51) - ( Б-56) с последующим перемножением матриц. [5]
Составим матрицу гамильтониана в базисе функций /, k, т) симметричного волчка. [6]
При построении матрицы гамильтониана циклической системы надо учитывать взаимодействия центрального атома с теми атомами, которые попадают внутрь ячейки Внгнера - Зейтца, что и определяет Kn: R. Введение Rn позволяет обеспечить эквивалентность атомов, расположенных в центре и на краях W-атомной цепочки. При этом некоторые взаимодействия приходится исключить вообще. [7]
Теперь в матрице гамильтониана появятся недиагональные члены, так как функции MS, Mj) не являются собственными функциями этого оператора. [8]
В методе МОХ матрица гамильтониана идентична топологической матрице молекулы, которая имеет единичные элементы в положениях, отвечающих связям С-С, и нулевые элементы во всех остальных положениях. [9]
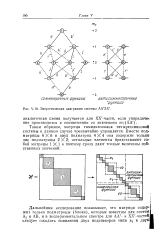 |
Энергетическая диаграмма системы АА ХХ. [10] |
Таким образом, матрица гамильтониана четырехспиновой системы в данном случае чрезвычайно упрощается. [11]
Это означает, что матрица гамильтониана эрмитова. [12]
Ранее утверждалось, что матрица гамильтониана, приведенная на рис. 3.4, эквивалентна матрице, заданной табл. 3.1, и поэтому энергетические зоны, показанные на рис. 3.8, а, совпадают с энергетическими зонами, рассчитанными точными методами. [13]
При / 0 блок матрицы гамильтониана имеет размерность 1 X 1 и содержит волновые функции / k 0 базисного набора. [14]
Этот метод позволяет свести матрицу гамильтониана к двум матрицам, из которых одна построена на состояниях валентной зоны, а другая - на состояниях зоны проводимости. Эти матрицы не связаны между собой и могут быть диагонализованы независимо друг от друга. Тем не менее можно ( показать, что такая диаго-нализация 1не изменяет сумму диагональных матричных элементов - Таким образом, сумму всех энергий в валентных зонах можно найти, не производя диагоналйзацию матрицы. Поэтому, даже если матрица гамильтониана имеет размерность 1023ХЮ23, энергию можно толучить последовательным суммированием ло связям, а изменение энергии, обусловленное деформацией связей, можно рассчитать, учитывая только те связи, которые затронуты этой деформацией. Эти следствия вытекают из следующего математического утверждения: при унитарных преобразованиях след матрицы гамильтониана не изменяется. [15]
Страницы: 1 2 3 4