Матрица - грам
Cтраница 2
Эту матрицу называют матрицей Грама билинейной формы. [16]
Для рассматриваемых месторождений составлены матрицы Грама и найдены коэффициенты а. В табл. 16 и 17 представлены значения коэффициентов а -, входящие в уравнение многомерных статистических моделей соответственно для пласта Дх Туймазин-ского месторождения и НГДУ Первомайнефть в целом. [17]
В программе 4.3 F матрица Грама А формируется с помощью подпрограммы GRAM, входными параметрами которой являются переменные N и М - количество узлов и базисных функций соответственно; L - условное число, определяющее тип базиса; X и F - массивы узлов и значений аппроксимируемой функции в них. [18]
Для произвольного базиса вводится матрица Грама - матрица Г, составленная из попарных скалярных произведений базисных векторов. [19]
Выясним, как связаны матрицы Грама форм w ( x, у) w ( Bx, y) и формы w ( x y) в некотором базисе. Пусть w ( x y) x G y, где у - вектор-столбец, составленный из координат вектора у в некотором базисе, [ х ] - вектор-строка. [20]
Действительно, так как матрица Грама системы элементов, союзной для сильно минимальной, ограничена и ряд (3.13) сходится, то по теореме 3 § 2 биортогональный ряд ( II) сильно сходится. [21]
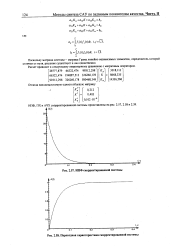 |
ИПФ скорректированной системы.| Переходная характеристика скорректированной системы. [22] |
Поскольку матрица системы - матрица Грама линейно независимых элементов, определитель которой отличен от нуля, решение существует и оно единственно. [23]
Если при каком-либо представлении матрицы Грама (2.2) системы элементов (2.1) в виде Ф DQD, где Q - ограниченная неотрицательная эрмитовская матрица, a D - чисто диагональная матрица с положительными элементами на главной диагонали, нуль является собственным значением матрицы Q, то система элементов (2.1) неминимальна. [24]
Указание: используйте связь матриц Грама двух базисов для случая, когда один из них - ортонормированный. [25]
Доказать, что определитель матрицы Грама любой конечной линейно независимой системы векторов линейного пространства со скалярным произведением положителен. [26]
В обоих случаях элементы матрицы Грама представляют собой скалярное произведение векторов из упомянутых последовательностей. Когда оба аргумента t и со принимают лишь счетное множество значений, процесс Y ( t, со) представляет собой матрицу чисел Y ( / -, со -), в которой элементы i - й строки указывают возможные значения процесса в момент / -, а элементы / - го столбца представляют собой последовательность чисел, которую пробегает / - я дискретная реализация случайного процесса. [27]
Для ортогональной системы элементов (2.1) матрица Грама является диагональной. [28]
Отметим, что так как матрица Грама определяет лишь нормы элементов системы и углы между ними, то существует бесконечно много систем элементов, для которых данная матрица Ф является матрицей Грама. [29]
Эти результаты формулируются в терминах матриц Грама и их доказательства основываются на теореме Перрона - Фробениуса о матрицах с неотрицательными элементами. [30]
Страницы: 1 2 3 4