Переходная матрица - состояние
Cтраница 1
Переходная матрица состояния обладает некоторыми другими свойствами. [1]
Переходная матрица состояния Ф ( 0 - Матричная экспоненциальная функция, описывающая свободное движение системы. [2]
Следовательно, переходную матрицу состояния можно представить в виде еА - o) f как уже было показано выше. [3]
Другими словами, дискретная переходная матрица состояния описывает движение состояний системы и является аналогом переходной матрицы состояния, определенной выше для системы с непрерывным временем. [4]
Преимущества сигнального графа при получении переходной матрицы состояния становятся очевидными, если рассмотреть преобразование Лапласа уравнения (3.72), считая входные сигналы равными нулю. [5]
Ниже мы установим некоторые свойства переходной матрицы состояния периодической системы. [6]
Подчеркнута важность таких фундаментальных понятий, как переходная матрица состояния и весовая функция динамической системы, лежащих в основе интегральной формы представления функциональных операторов ФХС, которая, как будет показано ниже ( см. гл. [7]
Решение линейных уравнений состояния осуществлялось с помощью переходной матрицы состояния, которая для стационарных систем имеет специальный вид. [8]
Таким образом, найден другой способ определения переходной матрицы состояний дискретной системы. [9]
Если, кроме сформулированного выше требования, норма переходной Матрицы состояния стремится к нулю при t, стремящемся к бесконечности, система является асимптотически устойчивой. [10]
Отсюда легко можно видеть, что для того чтобы определить переходную матрицу состояния, необходимо начальные значения всех переменных состояния кроме одной положить равными нулю и вычислить реакцию каждой переменной состояния на это ненулевое значение. Иначе говоря, элемент цу ( f) представляет собой реакцию / - й переменной состояния на начальное значение у - й переменной состояния при условии, что начальные значения всех остальных переменных состояния равны нулю. [11]
Сравним теперь точное значение реакции системы, полученное в предыдущем разделе с помощью переходной матрицы состояния, с приближенным значением, вычисленным в результате дискретизации времени. В табл. 3.1 приведены вычисленные точные значениях, ), атакже приближенные значения при Т 0 2 с и при Г 0 1 с. В случае Т 0 2 с ошибка остается приблизительно постоянной и равной 0 07, что составляет 7 % от начального значения переменных состояния. При уменьшении Т до 0 1 с ошибка также уменьшается приблизительно до 3 5 % от начального значения переменных состояния. Если взять Т 0 05 с, то аппроксимация решения в момент / 0 2 с дает значение X ( t) 0 655, и ошибка уменьшается до 1 5 % от начального значения переменных состояния. [12]
Вычисление временных характеристик линейных систем легко производится путем либо ( 1) использования переходной матрицы состояния, либо ( 2) с помощью дискретной аппроксимации уравнения состояния. Для нелинейных систем наиболее подходящим является метод дискретизации уравнения состояния, тем более, что он очень удобен при численных вычислениях на компьютере. [13]
Предоставляем читателю возможность доказать, что еА ( - о) обладает всеми свойствами переходной матрицы состояния. [14]
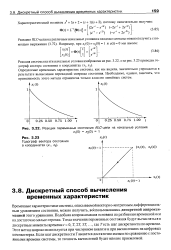 |
Реакция переменных состояния /. АС-цепи на начальные условия. [15] |
Страницы: 1 2 3