Переходная матрица - состояние
Cтраница 2
Определение временных характеристик системы, как мы видели, значительно упрощается в результате вычисления переходной матрицы состояния. Необходимо, однако, заметить, что применимость этого метода ограничена только классом линейных систем. [16]
Другими словами, дискретная переходная матрица состояния описывает движение состояний системы и является аналогом переходной матрицы состояния, определенной выше для системы с непрерывным временем. [17]
Матрица Хф ( /) Хф ( т) Ф ( / т) называется переходной матрицей состояния. [18]
Матричная экспоненциальная функция Ф ( г) описывает свободное движение системы и называется фундаментальной матрицей или переходной матрицей состояния. [19]
Если известны начальные условия х ( 0), вектор входных воздействий и ( /) и переходная матрица состояния Ф ( Г), то реакция системы х ( г) может быть вычислена тем или иным способом. Таким образом, задача сводится к вычислению матрицы Ф ( 0, которая в основном и определяет реакцию системы. Один из способов вычисления переходной матрицы состояния базируется на использовании сигнального графа системы. [20]
Вычислим временные характеристики Л1С - цепи с помощью дискретной аппроксимации уравнения состояния, не прибегая к определению переходной матрицы состояния. [21]
Матрицу Кх ( t, т) ехр [ A ( t - TJ, представляющую фундаментальную матрицу решений системы (5.34), принято называть переходной матрицей состояния динамической системы. [22]
О) определяется с помощью формулы Мейсона по сигнальному графу. Все элементы переходной матрицы состояния, cp Cs), могут быть получены путем установления связи между X s) и х ( 0) по структуре сигнального графа. Данный способ определения переходной матрицы состояния иллюстрирует следующий пример. [23]
В данном разделе рассматриваются вопросы о присоединенном представлении локальной однопараметрической группы преобразований с использованием формулы Бейкера-Кэмпбелла - Хаусдорфа, но в отличие от работ [28, 32] здесь она связывается с формулой Коши, широко применяемой в теории линейных систем. Данный подход позволяет получить локальный аналог переходной матрицы состояния для нелинейных аффинных систем управления. Напомним, что локальная однопараметрическая группа преобразований является представлением аддитивной группы вещественных чисел R на многообразии М в виде ее действий на элементы многообразия. Присоединенное представление дает возможность реализовать конструктивный алгоритм нахождения этого действия. [24]
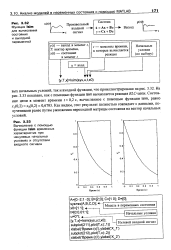 |
Функция Isim для вычисления состояния и выходной переменной. [25] |
На рис. 3.33 показано, как с помощью функции Isim вычисляется реакция / ЛС-цепи. Как видим, этот результат полностью совпадает с данными, полученными ранее путем умножения переходной матрицы состояния на вектор начальных условий. [26]
Теперь мы можем сформулировать основной результат, определяющий взаимодействие двух однопараметрических групп преобразований, выраженное через присоединенное представление. Хотя это взаимодействие определяется хорошо известной формулой Бейкера-Кэмпбелла - Хаусдорфа [14, 26, 28], вывод ее на основе присоединенного представления показан впервые, что, в свою очередь, позволяет дать новую геометрическую трактовку взаимодействия однопараметрических групп преобразований [13] и связать данную формулу с формулой Коши для линейных систем, а также получить локальный аналог переходной матрицы состояний для нелинейных аффинных систем. [27]
О) определяется с помощью формулы Мейсона по сигнальному графу. Все элементы переходной матрицы состояния, cp Cs), могут быть получены путем установления связи между X s) и х ( 0) по структуре сигнального графа. Данный способ определения переходной матрицы состояния иллюстрирует следующий пример. [28]
Если известны начальные условия х ( 0), вектор входных воздействий и ( /) и переходная матрица состояния Ф ( Г), то реакция системы х ( г) может быть вычислена тем или иным способом. Таким образом, задача сводится к вычислению матрицы Ф ( 0, которая в основном и определяет реакцию системы. Один из способов вычисления переходной матрицы состояния базируется на использовании сигнального графа системы. [29]
Отметим, что любую систему можно считать свободной, если входная переменная фиксирована. Функция ф ( 1 х0, t0) называется переходной функцией состояния системы. Она является обобщением ( на нелинейный случай) переходной матрицы состояния линейной системы. [30]
Страницы: 1 2 3