Трехдиагональная матрица

Cтраница 2

Полученная система уравнений характеризуется трехдиагональной матрицей. Следовательно, для решения такой системы алгебраических уравнений реализуется рассмотренный ранее метод прогонки. [16]

Простейший пример такой матрицы - трехдиагональная матрица - был указан выше. [17]

Линейная система уравнений (2.46) имеет трехдиагональную матрицу. [18]

Ленточная матрица и ее разложение. [19]

Системы Ах - Ь с трехдиагональными матрицами решаются почти мгновенно. [20]

Для численного решения систем с трехдиагональными матрицами применяется метод прогонки, который представляет собой вариант метода последовательного исключения неизвестных. [21]

Система алгебраических уравнений (5.80) характеризуется трехдиагональной матрицей. [22]

С ] & 0 называется трехдиагональной матрицей. [23]

Для решения систем ЛАУ с трехдиагональными матрицами коэффициентов используют разновидность метода Гаусса, называемую методом прогонки. Обозначим преобразованные по (5.4) значения ац и Ь через Г и qf соответственно. [24]

Система линейных алгебраических уравнений (7.55) с трехдиагональной матрицей может быть решена методом прогонки ( см. гл. [25]

Лг-1, возникает система уравнений, имеющая трехдиагональную матрицу. Эта система уравнений решается прогонки методом. [26]

Это линейная система относительно неизвестных, имеющая трехдиагональную матрицу с преобладанием диагональных элементов; ее решение легко вычисляется прогонкой. [27]

Пусть Т ( т, б) - трехдиагональная матрица, полученная соединением m копий Т0, как показано на рисунке. [28]

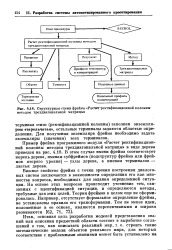Структурная схема фрейма Расчет ректификационной колонны методом трехдиагональной матрицы. [29]

Пример фрейма программного модуля Расчет ректификационной колонны методом трехдиагональной матрицы в виде дерева приведен на рис. 4.18. В этом случае имени фрейма соответствует корень дерева, именам субфреймов ( подструктур фрейма или фреймов второго уровня) - узлы дерева, а именам терминалов - листья дерева. [30]

Страницы: 1 2 3 4