Метод - продолжение - решение
Cтраница 1
Метод продолжения решения по параметру является наиболее универсальным. [1]
Метод продолжения решения по параметру в изложенном здесь виде может быть практически без изменений распространен на нелинейные краевые задачи, если считать, что F ( XP) представляет оператор краевой задачи, включающий ее уравнения и граничные условия, а дифференцирование в соотношениях ( В. [2]
Метод продолжения решения по параметру универсален и всегда приводит к решению X, однако для систем с несколькими устойчивыми состояниями может быть получено решение X, соответствующее точке неустойчивого равновесия. [3]
Метод продолжения решения по параметру применительно к обратной задаче динамики упругих систем / / Сопротивление материалов и теория сооруж. [4]
Использование методов продолжения решения по параметру при исследовании упруго-пластических деформаций естественным образом определяется самой постановкой задачи, которая подразумевает прослеживание истории деформирования системы. В этом смысле представляется закономерным, что первое применение метопа продолжения [452] связано именно с анализом устойчивости упругопластического стержня. [5]
Общая формулировка метода продолжения решения по параметру для нелинейных деформируемых систем была высказана в двух работах [276, 232], которые определили две различные формы метода. [6]
Различные схемы метода продолжения решения, в том числе метод в форме Д.Ф. Давиденко, обсуждаются в работе [304] с точки зрения организации итерационных процессов при шаговом подходе к решению нелинейных задач. [7]
Изложенные выше формы метода продолжения решения по параметру предполагают, что в рассматриваемом интервале значений параметра Р0 Р Р определитель det ( /) матрицы Якоби системы уравнений ( В. Использование метопа в окрестности особых точек, где det ( /) 0, требует особого обсуждения. Рассмотрим этот вопрос на примере алгебраической или трансцендентной системы уравнений. [8]
При таком применении метода продолжения решения к одномерным нелинейным краевым задачам они сводятся к последовательности одномерных линейных краевых задач, которые являются удобным объектом для решения методами типа прогонки. [9]
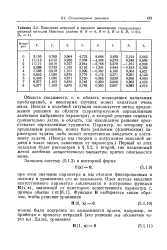 |
Поведение итераций в процессе вычисления стационарных решений методом Ньютона ( задача 8. N 4, А 2, В 6, Л, 0 4. [10] |
Иногда в подобной ситуации используется метод продолжения решения из области ( характеризуемой определенным значением выбранного параметра), в которой решение отыскать сравнительно легко, в область, где нахождение решения представляет определенные трудности. Параметр, по которому мы продолжаем решение, может быть реальным ( физическим) параметром задачи, либо может искусственно вводиться в постановку задачи. Иногда мы говорим о погружении исходной задачи в класс задач, зависящих от параметра. Первый из этих подходов будет рассмотрен в § 5.2, а второй, так называемый метод введения искусственного параметра, кратко описывается ниже. [11]
Следует отметить, что применение метода продолжения решения непосредственно к уравнениям краевой задачи не связывает его численную реализацию с каким-либо конкретным способом алгебраизации исходной задачи и открывает возможности использования самых различных методов для решения пошаговых линейных краевых задач. [12]
Большое число исследований связано с применением метода продолжения решения к классической нелинейной задаче конечных и больших прогибов оболочек вращения. [13]
В статье [61] сравниваются различные формы метода продолжения решения: явная схема метода Эйлера, схема типа предиктор-корректор, дискретное продолжение с использованием для итерационного уточнения решения, модифицированного метода Ньютона. На простом примере оценена их погрешность. [14]
Решение нелинейной задачи выполняется на основе метода продолжения решения по параметру и одношаговой модификации алгоритма Ньютона-Канторовича. На каждом шаге вычис: лительного процесса происходит пересчет метрики деформированной срединной поверхности оболочки. При этом используется метод Лагранжа, согласно которому вводится координатная система, вмороженная в тело оболочки. [15]
Страницы: 1 2 3