Бартлетта

Cтраница 2

Бартлетт доказал, что, если нулевая гипотеза (4.2.4.6) справедлива, то случайная величина (4.2.4.7) при п - оо имеет асимптотическое распределение хи - квадрат с т - 1 степенями свободы. [16]

Бартлетт ставит опыт и при комнатной температуре из газообразного гексафторида платины и газообразного ксенона получает твердое оранжево-желтое вещество - гексафторплатинат ксенона XePtFe, поведение которого ничем не отличается от поведения обычных химических соединений. [17]

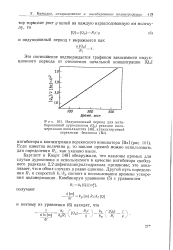Индукционный период для инги-бированной дурохиноном ( Q0 реакции полимеризации винилацетата, катализируемой перекисью бензоила ( Bz. [18]

Бартлетт и Кварт [48] обнаружили, что наклоны прямых для случая дурохинона и используемого в качестве ингибитора свободного радикала 2 2-дифенилпикрилгидразила одинаковы; это показывает, чтов обоих случаях у равно единице. Другой путь определения RI и скоростей ktlkp состоит в использовании времени ускорения полимеризации. [19]

Бартлетт и Нодзаки [40] при сравнительном изучении распада перекиси бензоила в различных растворителях нашли, что скорость распада перекиси бензоила в первичных, вторичных и третичных аминах, за отдельными исключениями, протекает с очень большой скоростью, большей, чем в каких-либо других средах. [20]

Бартлетт и Тарбелл [32] считают, что вторая стадия реакции проходит очень быстро и возникающие катионы не успевают присоединить одну и ту же плоскую конфигурацию. [21]

Бартлетт, работавший с новым соединением, гексафторидом платины ( PtF6), обнаружил, что это вещество является отличным захватчиком чужих электронов; почти столь же сильным, как фтор. Гексафторид платины мог отобрать электроны даже у кислорода, который проявляет существенно большую склонность к присоединению дополнительных электронов, чем к их отдаче. А если PtF6 сумел отобрать электроны у кислорода, то имелся шанс, что это он Справится и с ксеноном. [22]

Бартлетт ставит опыт и при комнатной температуре из газообразного гексафторида платины и газообразного ксенона получает твердое оранжево-желтое вещество - гексафторплатинат ксенона XePtF6, поведение которого ничем не отличается от поведения обычных химических соединений. [23]

Бартлетт ( Bartlett, 1951) указал, что реакционная способность может также снижаться ( в таких структурах, как XII-XIV) в результате пространственной затрудненности сольватации, обусловленной большими размерами реагирующей молекулы. [24]

Бартлетт и Коэн [108] экспериментально доказали наличие в молекуле полистирола, заполимеризованного при помощи перекисей - хлор - и и-бромбензоила, радикалов галоидфенила и галоидбензоила. [25]

Бартлетт исследовал в качестве донора гидрид-иона этиловый, н-пропиловый, изопропиловый, етор-бутиловый, изобутило-вый, а-метилизобутиловый спирты, пинакон, а также диэтило-вый и диизопропиловый эфиры. Способность к отдаче гидрид-иона непосредственно связана с основностью: чем меньше основность спирта ( эфира), тем меньше склонность к образованию оксониевого соединения и, следовательно, больше склонность к отдаче гидрид-иона. [26]

Бартлетт Нил 1962 Бартолин Каспар мл. [27]

Метод Бартлетта и Шнейдера был применен для синтеза соответствующего кетона и спирта при конденсации mjDem - бутилхлорида и метилового эфира триметилуксусной кислоты в присутствии натрия. [28]

Критерий Бартлетта весьма чувствителен к отклонениям распределении от нормального, поэтому к выводам, полученным по этому критерию, надо относиться осторожно. [29]

Критерий Бартлетта, как правило, используется для проверки равноточности более двух серий измерений. Для проверки равно-точности двух серий измерений пользуются критерием дисперсионного отношения. Требуется проверить, согласуются ли полученные значения sf и si с некоторой гипотезой Я0, согласно которой дисперсии выборок находятся в заданном отношении к. Когда с гипотезой Н0 конкурирует гипотеза Я1 ( согласно которой ajYai к, то в качестве критического значения для отношения sf / sl выбирают функцию кР ( Q; Vi, v2), где Q - заданный уровень значимости, выраженный в процентах, Если sf / si кР ( Q; vx; v2), то гипотезу Я0 следует отвергнуть. [30]

Страницы: 1 2 3 4