Наклон - фазовая траектория
Cтраница 1
Наклон фазовой траектории к оси абсцисс для каждой изоклины на рис. 236 показан отрезками прямых, проведенных соответственно под углами arctgm и arctgn. Эти отрезки являются касательными к фазовой траектории. [1]
Наклон фазовой траектории к оси абсцисс для каждой изоклины на рис. 236 показан отрезками прямых, проведенных соответственно под углами arctg / л и arctgra. Эти отрезки являются касательными к фазовой траектории. [2]
Но по построению наклон фазовой траектории в точке В равен наклону луча О А, следовательно. [3]
 |
Принципиальные схемы нелинейных систем автоматического регулирования. а - давления в ресивере. б - релейной следящей системы. [4] |
Далее необходимо определить наклон фазовой траектории в начальной и последующих точках. Из точки Р г на оси х и у соответственно опускают перпендикуляры, пересекающие ось х в точке Q, а ось у в точке R. [5]
Он совпадает с наклоном фазовой траектории в точке Р1 ( поэтому из F, как из центра, радиусом РР с. Плавность фазовой траектории зависит от длины элемента окружности и может быть улучшена путем использования более коротких дуг. Аналогично, выбирая в качестве начальных точки Ра и Р3, получим решение задачи в виде траекторий / / и / / /, изображенных на рис. 5.5. На основании выполненного построения можно сделать вывод о том, что все фазовые траектории скручиваются к началу координат, которое является особой точкой типа устойчивого фокуса. Последнее доказывает асимптотическую устойчивость данной нелинейной системы. [7]
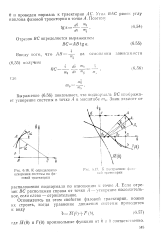 |
К определению ускорения системы по фазовой траектории. [8] |
Угол ВАС равен углу наклона фазовой траектории в точке А. [9]
Выражение ( 5) определяет наклон фазовой траектории в данной точке. [10]
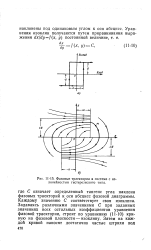 |
Фазовые траектории в системе с нелинейностью гистерезисного типа. [11] |
С означает определенный тангенс угла наклона фазовых траекторий к оси абсцисс фазовой диаграммы. Каждому значению С соответствует своя изоклина. Задаваясь различными значениями С при заданных значениях всех остальных коэффициентов уравнения фазовой траектории, строят по уравнению ( 11 - 10) кривую на фазовой плоскости - изоклину. [12]
Выражение ( 5) определяет - наклон фазовой траектории в данной точке. [13]
При YwJ и тпхг 1ПуГ угол наклона фазовой траектории к оси остается приблизительно таким же, как и в случае отсутствия вязкого трения. Таким образом, при сделанных допущениях вязкое трение не вносит существенных изменений в характер движения изображающей точки фазового портрета рис. 5.27, что находится в противоречии с действительной картиной движения главной оси быстровращающегося твердого тела при наличии диссипативных моментов. [14]
На каждой изоклине нанесены линии, указывающие наклон фазовой траектории arctgN, когда она пересекает данную изоклину. [15]
Страницы: 1 2 3
