Стационарное автоколебание

Cтраница 2

Рассмотрим следующий вопрос: на какой частоте и с какой амплитудой происходят стационарные автоколебания системы электронный поток - резонатор. [16]

Последующее увеличение интенсивности помех по сравнению с величиной Л и 5 ( амплитудой стационарных автоколебаний в автономных ВЧ) приводит не только к срыву синхронизации, но и к подавлению автоколебаний в ВЧ. [17]

Это выражение определяет u ( t) при колебаниях маятника, близких к стационарным автоколебаниям. [18]

Будем искать приближенное решение этого уравнения, предполагая, что колебательное движение маятника приближается к стационарным автоколебаниям. В этом случае амплитуда колебаний маятника должна мало отличаться от постоянной величины. [19]

Вращающийся вал мотора сообщает маятнику энергию, необходимую на покрытие потерь энергии на тепло при стационарных автоколебаниях. Энергия передается от мотора к маятнику силой трения скольжения. Из всех рассуждений очевидно, что частота автоколебаний определяется собственной частотой колебаний маятника. Опыт показывает, что частота автоколебаний и в других случаях близка к собственной частоте резонатора, который входит в состав колебательной системы. [20]

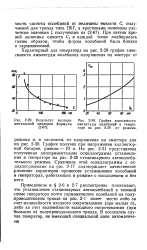Результат экспери - [ IMAGE ] - 30. График зависимости. [21]

Приведенное IB § 2 - 6 и 2 - 7 ( рассмотрение показывает, что установление стационарных автоколебаний в типовой схеме генератора почти гармонических колебаний на полупроводниковом триоде на рис. 2 - 1 имеет место либо за счет нелинейности входного сопротивления ( при малых п), либо за счет нелинейности выходного сопротивления ( при больших п) полупроводникового триода. [22]

Поэтому и в этом частном примере при коммутирующем режиме работы усилителя-коммутатора в часах имеет место один устойчивый режим стационарных автоколебаний. [23]

Известно, что еще в процессе проектирования часов их параметры выбираются так, чтобы обеспечить достаточный запас устойчивости стационарных автоколебаний. [24]

Полученное распределение о ( Дф) позволяет в качестве частного случая получить распределение амплитуд колебаний в часах при отсутствии стационарных автоколебаний - амплитуд вынужденных колебаний системы баланс - спираль около положения статического равновесия ф 0 под действием случайных угловых вибраций. [25]

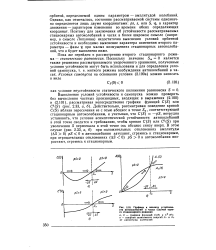Графики к анализу устойчивости автоколебаний в часах ( случай одного стационарного режима. [26]

Действительно, рассматривая поведение кривой C ( S) вблизи пересечения ее с осью абсцисс в точке S, соответствующей стационарным автоколебаниям, и учитывая, что C ( S) - pS, нетрудно установить, что условие асимптотической устойчивости автоколебаний в этой точке сводится к требованию, чтобы кривая C ( S) или C ( S) при увеличении S пересекала в этой точке ось абсцисс снизу вверх. В этом случае ( рис. 2.33, а, б) при положительных отклонениях амплитуды ( AS 0) pS 0 и автоколебания затухают, стремясь к стационарным, при отрицательных отклонениях ( AS 0) pS 0 и автоколебания возрастают, стремясь к стационарным. [27]

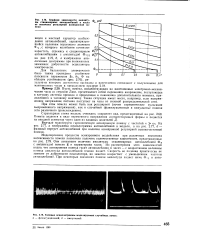Графики зависимости амплиту - ф ад ды стационарных автоколебаний в часах г.| Типовые осциллограммы моделируемых случайных помех. [28]

Моделирование процессов асинхронного воздействия при различных значениях интенсивности помехи позволило получить количественные зависимости, представленные на рис. 2.78. Они связывают величину амплитуды стационарных автоколебаний Ф с амплитудой помехи 5 и параметрами часов. Из рассмотрения этих зависимостей видно, что асинхронная помеха гасит автоколебания в часах - с возрастанием величины помехи амплитуда автоколебаний плавно падает. Скорость ее падения практически не зависит от добротности осциллятора, но заметно возрастает с уменьшением частоты автоколебаний. [29]

Схема генератора, работающего в активной области полупроводникового триода. [30]

Страницы: 1 2 3 4