Стационарное автоколебание
Cтраница 1
Установление стационарных автоколебаний математически описывается как притяжение траектории к предельному циклу. Физически это притяжение может быть понято следующим образом. Каков бы ни был конкретный механизм диссипации и подачи энергии, энергия из некоторого источника, обычно неколебательного, преобразуется в колебательное движение. Обычно, чем больше амплитуда колебаний, тем больше потребление энергии от источника. С другой стороны, количество рассеянной энергии также зависит от амплитуды. Эти зависимости определяют амплитуду стационарных колебаний, как показано на рис. 2.8. Если колебаний нет ( амплитуда равна нулю), то нет ни потерь энергии, ни потребления энергии от источника; следовательно, обе функции должны проходить через начало координат. Пересечение этих двух кривых определяет амплитуду А стационарных колебаний. В этой точке поступление энергии в точности компенсирует ее потери. [2]
В некоторых случаях стационарные автоколебания носят почти гармонический характер и совершаются с частотой свободных колебаний системы; соответствующие системы называются квазилинейными. В других случаях стационарные автоколебания резко отличаются от гармонических, сопровождаются остановками и скачками скорости; такие автоколебания ( и соответствующие системы) называются релаксационными или разрывными. [3]
Для орбитной устойчивости рассматриваемых многопараметрических стационарных автоколебаний требуется, чтобы решения всех уравнений системы ( 2.103 6) стремились с течением времени к нулю. [4]
Выше было сказано, что определение частоты стационарных автоколебаний формулой (11.241) следует рассматривать как некоторую гипотезу. [5]
 |
Энергетические уровни ионов хрома в рубине. [6] |
Для возникновения и поддержания в квантовом генераторе стационарных автоколебаний должен поддерживаться баланс мощностей, а именно, равенство мощности, отданной активным веществом, и мощности всех видов потерь. Мощность, отданная на выбранном рабочем переходе, определяется согласно ф-ле (8.20) разностью населенностей уровней пг - nlr а значит, и интенсивностью накачки. Следовательно, существует минимальная пороговая величина энергии накачки Wm. Расчеты показывают, что если накачка производится на длине волны 0 56 мкм, а концентрация ионов хрома в рубине равна 0 03 %, то пороговая энергия накачки для единицы объема кристалла составляет Wa. Эта энергия должна быть передана кристаллу за время, меньшее времени жизни частиц на уровне 2, чтобы его населенность не успела снизиться из-за релаксации. [7]
Обычно по истечении времени Т в системе устанавливаются стационарные автоколебания. Если исходным реагентом является неСс4, а смесь Се3 и Се14 в отношении, соответствующем установившемуся колебательному режиму, то колебания в системе начинаются сразу. [8]
Степень выполнения последних неравенств определяет величину запаса устойчивости стационарных автоколебаний в часах. [9]
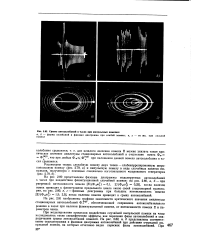 |
Срывы автоколебаний в часах при импульсных помехах. [10] |
На рис. 2.81 изображены графики зависимости критического значения амплитуды стационарных автоколебаний Ф кр, обеспечивающей сохранение автоколебательного режима в часах при наличии флюктуационной помехи, от интенсивности помехи S и параметров часов. [11]
Рассмотрим возможные режимы автоколебаний в часах и прежде всего режим устойчивых стационарных автоколебаний, наличие которых является необходимой предпосылкой работы часов. [12]
 |
Фазовая диаграмма колебаний в часах ( случай единственного стационарного режима. [13] |
На рис. 2.34 изображена фазовая диаграмма рассмотренного выше простейшего случая единственных стационарных автоколебаний в часах, устойчивых и имеющих самопуск - мягкий режим возбуждения автоколебаний. Стационарным автоколебаниям с амплитудой S соответствует замкнутая фазовая траектория ( предельный цикл) - окружность с радиусом S которая образована непрерывно движущейся изображающей точкой С с угловой скоростью pty в направлении по часовой стрелке. [14]
Особенности режима насыщения полупроводникового триода в ряде случаев определяют характер установления стационарных автоколебаний в генераторах. Поэтому нелинейность генератора почти гармонических колебаний, работающего в режиме с насыщением, не может считаться малой, что требует применения при теоретическом исследовании такого генератора одного из методов анализа импульсных систем. [15]
Страницы: 1 2 3 4
