Устойчивое автоколебание

Cтраница 4

Характер зависимости амплитуды А периодического решения уравнения движения типового гидравлического следящего привода с нелинейностями сухого трения в рабочем органе привода и насыщения перепада давления. [46]

Если начальные амплитуды или внешние возмущающие воздействия больше величины неустойчивых амплитуд Ан, то в следящем приводе устанавливаются устойчивые автоколебания, амплитуда Ау которых определяется верхней кривой. [47]

Если картина фазовых траекторий имеет устойчивый предельный цикл, это свидетельствует о том, что рассматриваемая система обладает устойчивыми автоколебаниями. Размеры предельного цикла по оси х определяют амплитуду колебаний, а по оси у скорость изменения амплитуды. [48]

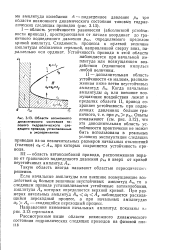Области возможного динамического состояния типового гидравлического сле-цящего привода, установленные в экспериментах. [49]

Если начальные амплитуды или внешние возмущающие воздействия ао больше величины неустойчивых амплитуд Ан, то в следящем приводе устанавливаются устойчивые автоколебания, амплитуда Ау которых определяется верхней кривой. При размерах начальных амплитуд Ан а0 Ау наблюдается расходящийся переходный процесс, а при начальных амплитудах а0 Ау - сходящийся переходный процесс. [50]

Система этих уравнений позволяет определить амплитуду и частоту периодического решения для ошибки слежения и выделить области устойчивости равновесия и устойчивых автоколебаний для любого конкретного следящего привода. [51]

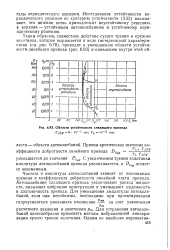Области устойчивости следящего привода. [52]

Исследование устойчивости периодического решения по критерию устойчивости (3.52) показывает, что нижняя ветвь принадлежит неустойчивому решению а верхняя - устойчивым автоколебаниям и устойчивому периодическому решению. [53]

В первом случае мы убеждаемся, что система имеет устойчивый предельный цикл, что свидетельствует о возможности возникновения в системе устойчивых автоколебаний. [54]

Из условия ( 111 26) определяем значение передаточной функции нелинейного элемента и по графику Wn ( A) находим амплитуды устойчивых автоколебаний. Частота автоколебаний определяется как значение пары мнимых сопряженных корней характеристического уравнения. [55]

В нелинейных цепях постоянного тока ( не содержащих источников переменного напряжения или тока) может, как указывалось, существовать режим устойчивых автоколебаний. При этом получается замкнутая фазовая траектория, называемая предельным циклом. [56]

Если сдвинуть начало координат влево по кривой, то получим картину, показанную на рис. 1.5. При этом в системе будут происходить устойчивые автоколебания. [57]

В этой работе, в частности, выяснено, что в случае, когда функция / ( и) имеет один максимум, в системе возникают абсолютно устойчивые автоколебания возле этого максимума и что наличие дополнительных максимумов может привести к появлению невыгодных режимов работы. [58]

Последний вопрос возникает по следующей причине: поскольку прямолинейное поступательное торможение ( невозмущенное движение) неустойчиво по углу атаки и угловой скорости, возможны ли при этом устойчивые автоколебания в системе. [59]

Вид функции ниже ( а и выше ( б порога неустойчивости. [60]

Страницы: 1 2 3 4 5