Несмещенность

Cтраница 2

Требование несмещенности не определяет оценку однозначно. Чтобы получить единственную оценку из всех несмещенных, выбирают ту, которая имеет наименьшую дисперсию. Несмещенная оценка с наименьшей дисперсией называется эффективной. Следовательно, эффективная оценка по одной выборке дает значение в среднем наиболее близкое к 9, чем другие, оценки. [16]

Требование несмещенности особенно важно при малом объеме выборки. Для того чтобы использовать оценки, выведенные для каждой серии, и получить путем осреднения их более точную общую оценку, нужно быть уверенным в отсутствии систематического смещения у каждой частной оценки. Это будет тогда, когда частная оценка для каждой серии является несмещенной. [17]

Свойство несмещенности, однако, недостаточно характеризует оценку. [18]

Докажите асимптотическую несмещенность и состоятельность оценки Парзена в многомерном случае. Указание: доказательство проводится аналогично случаю одной переменной. [19]

Удовлетворение требованию несмещенности устраняет систематическую погрешность оценивания, которая, вообще говоря, зависит от объема выборки пив случае состоятельности оценки стремится, как правило, к нулю при п-оо. Если смещение оценки удалось выяснить, то оно легко устраняется. [20]

Удовлетворение требованию несмещенности устраняет систематическую погрешность, которая зависит от объема выборки п и в случае состоятельности стремится к нулю при п - - оо. [21]

Удовлетворение требованию несмещенности устраняет систематическую погрешность, которая зависит от объема выборки и и в случае состоятельности стремится к нулю при п - оо. [22]

В силу несмещенности оценки G величина У Gx служит несмещенной оценкой величины дх. [23]

Это означает асимптотическую несмещенность. [24]

Заметим, что несмещенность и состоятельность связаны друг с другом, но из первого не следует второго. [25]

Таким образом, несмещенность, эффективность и состоятельность являются независимыми свойствами оценок, характеризующими оценки с разных сторон. [26]

Принципы достаточности, несмещенности, инвариантности служат для сужения класса решающих правил. Они состоят в том, чтобы использовать в качестве решающих функций лишь соответственно достаточные, несмещенные и инвариантные решающие правила. Использование одного из этих принципов, двух из них или всех трех ( если это оказывается возможным) позволяет в ряде случаев настолько сузить класс рассматриваемых стратегий, что его пересечение с полным классом оказывается состоящим из одной-единственной решающей функции. Это означает, что в выделенном подклассе существует равномерно наилучшая стратегия ( ср. [27]

Поэтому достаточно доказать несмещенность M. [28]

Заметим, что несмещенность дисперсии на выходе восстанавливающего элемента нулевого порядка определяется тем ( см. например, рис. 9 и 15), что в этом случае кеждая ордината корреляционной функции восстановленного сигнала при т qTs равна соответствующей ординате корреляционной функции исходного сигнала. Действительно, соответствующая этому элементу корреляционная функция Reg ( T), участвующая в операции свертки, определяемой выражением (4.13), захватывает единственную ординату решетчатой корреляционной функции исходного еигнала. [29]

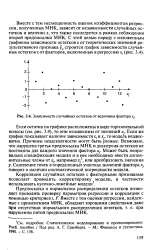Зависимость случайных остатков от величины фактора Xj. [30]

Страницы: 1 2 3 4