Конвективная неустойчивость

Cтраница 2

Условие (10.3) необходимо для развития конвективной неустойчивости, но не достаточно из-за неизбежного нарушения адиабатичности при движении элемента в среде. При адиабатическом расширении элемента в среде с dS / dr 0 его температура становится больше температуры среды и процессы теплопроводности стремятся ее выровнять, что стабилизирует конвективную неустойчивость. С другой стороны, вязкость замедляет движение элемента, что также дает стабилизацию. [16]

Таким образом, линейный анализ конвективной неустойчивости несжимаемой жидкости показал, что стационарная конвекция наступает при Ra RaKp. На плоскости хОу имеет место одномерная периодичность - система параллельных полос. Часто наблюдаемая трехмерная гексагональная ячеистая структура обусловлена, по-видимому, действием поверхностного натяжения в жидкости. [17]

В этом разделе обсуждаются необходимые условия конвективной неустойчивости в поле сил тяжести. [18]

В следующем параграфе будет произведен анализ конвективной неустойчивости и устойчивости течения Куэтта в линейном приближении. [19]

Стуррок [146, 147] пришел к выводу, что конвективная неустойчивость в основном связана с возмущениями такого же типа, как и пространственно нарастающие волны. При этом для системы уравнений, описывающих конвективную неустойчивость, решение в виде функций (11.2.26) может существовать лишь при определенной связи между о и а. Уравнение D ( a, a) - 0, при котором имеется решение, было названо дисперсионным. Существуют один или несколько корней этого дисперсионного уравнения, которые соответствуют нарастающим волнам; при этом со является действительным числом, а а - - комплексным. Был предложен критерий, который позволяет определить, затухает или нарастает возмущение. Однако этим критерием нелегко воспользоваться, если дисперсионное соотношение не представлено в явной форме. [20]

Их можно объяснить довольно просто с помощью конвективных неустойчивостей. [21]

Остановимся теперь кратко на результатах экспериментальных исследований конвективной неустойчивости вращающегося горизонтального слоя жидкости. [22]

Согласно [3-3, 3-25] ламинарно текущая пленка всегда обладает конвективной неустойчивостью относительно возмущений с длиной волны, намного большей толщины пленки. Наличие конвективной неустойчивости не означает невозможности осуществления ламинарного течения. При малых числах Рейнольдса возникающие в пленке возмущения сносятся вниз по течению и не приводят к образованию какого-либо устойчивого режима. Если же число Рейнольдса пленки больше некоторого предельного ReB ( H, то образуется устойчивый волновой режим. TiH такой режим невозможен. [23]

Неравенства ( 9) и являются условиями отсутствия конвективной неустойчивости. [24]

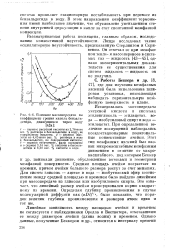Влияние массопередачи на. [25]

Рассматриваемая работа посвящена, главным образом, исследованию конвективной неустойчивости. [26]

Кроме описанной области неустойчивости, имеются также области конвективной неустойчивости, примыкающие к оси Ra. При отсутствии поперечной разности температур ( Gr 0) критические числа Рэлея, определяющие границы устойчивости равновесия, образуют дискретный спектр. При увеличении Gr эти критические числа изменяются ( линии 3 и 4 ] и происходит характерное замыкание нейтральных линий монотонных возмущений ( ср. [27]

В более поздней работе [86] результаты теоретического исследования конвективной неустойчивости псевдоожиженного слоя сопоставляются с экспериментальными данными. Отмечается, что теоретические и экспериментальные данные согласуются между собой. [28]

Нелинейное развитие и взаимодействие возмущений конечной амплитуды при конвективной неустойчивости вращающегося плоского слоя / / Докл. [29]

В заключение заметим, что если имеется система с конвективной неустойчивостью, замкнутая в кольцо, то в этом случае иногда говорят о глобальной неустойчивости. Примером системы с глобальной неустойчивостью является лампа бегущей волны с запаздывающей обратной связью, которая будет рассмотрена в последующих лекциях. [30]

Страницы: 1 2 3 4