Нормальность - распределение
Cтраница 1
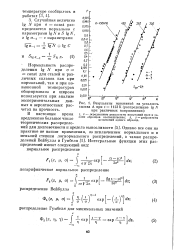 |
Результаты испытаний на усталость. [1] |
Нормальность распределения lg N при а const для сталей и различных сплавов как при нормальной, так и при повышенной температурах общепризнана и широко используется при анализе экспериментальных данных и вероятностных расчетах на прочность. [2]
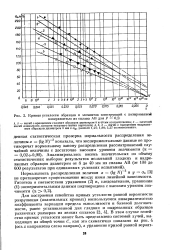 |
Кривые усталости образцов и элементов конструкций с полированной поверхностью из сплава АВ для Р 0 5. [3] |
Нормальность распределения величин х ( lg N) - - и у аа [3] не противоречит существованию между ними линейной зависимости. [4]
Нормальность распределения данных вектор-столбца у проверена в гл. [5]
Нормальность распределения данных вектора-столбца у проверена в гл. Таким образом, наблюдения роста и веса двадцатилетних мужчин являются двумерной нормально распределенной величиной и имеет место второй тип регрессии, при котором может быть исследована прямая у / ( х) и обратная х / ( /) регрессии и выполнен корреляционный анализ. [6]
Нормальность распределения данных вектор-столбца у проверена в гл. [7]
Нормальность распределения значений параметра х для шин каждой конструкции проверяют при помощи критериев согласия. Одним из таких критериев, позволяющих приближенно оценить нормальность распределения, являются неравенства35, вычисляемые отдельно для шин каждой конструкции. [8]
Однако нормальность распределения оценки в виде (7.5) является в высшей степени асимптотическим свойством. Это следует из того факта, что случайная переменная (7.24) распределена по нормальному закону для конечного числа наблюдений, только если A ( Xt) распределена также по нормальному закону: Даже если бы это выполнялось, то функция h в общем случае нарушала бы свойство нормальности при конечном числе наблюдений. [9]
Проверяют нормальность распределения результатов наблюдения. [10]
Проверяют нормальность распределения результатов наблюдений. [11]
Проверяем нормальность распределения результатов наблюдения. Ввиду того, что число наблюдений имеет незначительную величину ( п 18), то для проверки нормальности можно воспользоваться понятием статистической функции распределения результатов наблюдений. [12]
Оценим нормальность распределения записанных данных. [13]
К нормальности распределения аналитических данных не следует предъявлять слишком жестких требований, важно чтобы эти данные не имели ярко выраженной асимметрии. [14]
Проверка нормальности распределения согласно критерию х2 сводится к следующему. [15]
Страницы: 1 2 3 4