Нормальность - распределение
Cтраница 3
Проверяют гипотезу о нормальности распределения результатов наблюдения. [31]
Если предположение о нормальности распределения данных наблюдений грубо ошибочно, все же можно использовать непараметрические критерии ( критерии с произвольным распределением) до тех пор, пока существует независимость от выборки к выборке. Одно из свойств непараметрических критериев состоит в том, что для любого объема выборки распределение статистики проверки при нулевой гипотезе ( нет изменения) является существенно независимым распределением данных. Другими словами, существует постоянная вероятность ложной тревоги для независимо распределенных переменных. [32]
Следовательно, гипотеза нормальности распределения подтверждается и по этому критерию. Некоторое представление о близости эмпирического распределения к нормальному может дать анализ показателей асимметрии и эксцесса. [33]
Следовательно, гипотеза нормальности распределения выборки данных приведенных в табл. 1.1, принимается. [34]
Следовательно, гипотеза нормальности распределения выборки данных, приведенных в табл. 1.1, подтверждается. [35]
Следовательно, гипотеза нормальности распределения выборки данных приведенных в табл. 1.1, принимается. [36]
Следовательно, гипотеза нормальности распределения выборки данных приведенных в табл. 1.1, принимается. [37]
Если проверяется гипотеза о нормальности распределения, то к числу этих связей относится равенство среднего арифметического и точечной оценки дисперсии соответственно математическому ожиданию и дисперсии предполагаемого нормального распределения. Кроме того, всегда требуется, чтобы сумма частостеи по всем интервалам была равна единице. [38]
Если проверяется гипотеза о нормальности распределения, к числу этих связей относятся. [39]
Аналогично следует проанализировать на нормальность распределения все исходные данные. [40]
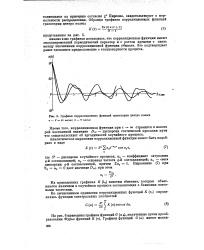 |
Графики корреляционных функций траектории центра колеса а - V 40 км / час. 6 - V км / час. [41] |
Пирсона, свидетельеадуют о нормальности распределения. [42]
При этом предположение о нормальности распределения возмущений оказывается несущественным. [43]
Критерий использует предположения о нормальности распределений случайных величин - моделей изучаемых геологических признаков в сравниваемых объектах, об отсутствии аномальных наблюдений и некоторые другие. [44]
Была выдвинута гипотеза о нормальности распределения случайной величины Дх, которая проверялась методом имитационного моделирования. Для проверки гипотезы использовался критерий согласия Колмогорова. [45]
Страницы: 1 2 3 4