Нукияма
Cтраница 1
 |
Типичная кривая распределения по размерам капелек тумана, полученного распылением жидкости. [1] |
Нукияма и Танасава90 исследовали также зависимость дисперсности генерируемого небольшими пневматическими распылителями тумана от условий их работы и физических свойств жидкости. [2]
Широко раслространена также формула Нукиямы и Танасавы. Ими использована зависимость ф а. [3]
Средний диаметр распыленных капелек дибутил-фталата, вычисленный по уравнению Нукиямы - Танасавы. [4]
Весовой медианный диаметр капель, представляющий в некоторых случаях больший интерес, чем средний объемно-поверхностный диаметр do, можно рассчитать из данных, полученных Льюисом и др. 91 путем обработки результатов опытов Нукиямы и Танасавы. [5]
Весовой медианный диаметр капель, представляющий в некоторых случаях больший интерес, чем средний объемно-поверхностный диаметр d0, можно рассчитать из данных, полученных Льюисом и др. 91 путем обработки результатов опытов Нукиямы и Танасавы. [6]
Мы видим, что отношение расстояния между каплями к диаметру капли зависит только от отношения объемных расходов воздуха и топлива в интересующей нас области. Нукияма и Таназава 18 ] при исследовании воздушного распиливания обнаружили, что если указанное отношение объемных расходов менее 5000, то наблюдается увеличение среднего диаметра капли. [7]
При исследовании конкретных систем были предложены и другие способы аналитического выражения распределения частиц по размерам. Так, Нукияма и Танасава15 вывели экспоненциальную формулу (2.20) для распределения по размерам капелек, образующихся при распылении жидкостей. [8]
При исследовании конкретных систем были предложены и другие способы аналитического выражения распределения частиц по размерам. Так, Нукияма и Танасава15 вывели экспоненциальную формулу (2.20) для распределения по размерам капелек, образующихся при распылении жидкостей. [9]
Увеличение перегрева стенки ведет к росту числа одновременно действующих центров парообразования, что сопровождается ростом интенсивности теплообмена. Для кипения характерна очень сильная зависимость плотности теплового потока q от перегрева стенки относительно температуры насыщения; это кардинально отличает теплообмен при кипении от однофазной конвекции и от конденсации. Нукияма, по имени японского исследователя, впервые описавшего эту зависимость в 1935 г. Типичная кривая кипения со схематическим изображением механизма теплообмена при различных сочетаниях плотности теплового потока и перегрева стенки А Т Тс - Ts представлена на рис. 8.3. Пусть жидкость в обогреваемом сосуде находится при температуре насыщения 7, отвечающей давлению ps над ее уровнем. Обогреваемая поверхность, например, в виде обращенной вверх пластины с адиабатной нижней поверхностью размещена под уровнем жидкости. По обеим координатным осям используется логарифмический масштаб. [10]
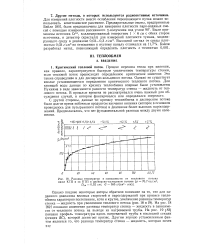 |
Разница температур в зависимости от теплового потока. [11] |
Процесс переноса тепла при кипении, как правило, характеризуется быстрым увеличением температуры стенки, если тепловой поток превосходит определенное критическое значение. Это также справедливо и для дисперсно-кольцевого потока. Однако не существует вполне установившегося определения критического теплового потока. Для кипящей воды данные по кризису теплообмена впервые были установлены Нукияма в виде зависимости разности температур стенка - жидкость от теплового потока. [12]
Страницы: 1