Другой нуль

Cтраница 1

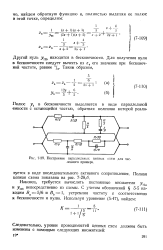Построение параллельных цепных схем для численного примера. [1]

Другой нуль у 26 находится в бесконечности. [2]

Других нулей, а также точек разрыва функция не имеет. На полупрямой ( 0, оо) функция является положительной. [3]

Других нулей, а также точек разрыва функция не имеет. На полупрямой ( 0, со) функция является положительной. [4]

Во всех других нулях т2 это условие сводится к нулю. Следовательно, полученный результат отличен от нуля. [5]

Я, 0) других нулей не имеет. [6]

Итак, многочлен P Q - - kPQ не имеет других нулей, кроме уже найденных, и значит, все его нули действительны. [7]

Лп) степени п 1, который не может иметь других нулей; все эти нули действительны и различны. [8]

Следовательно, в этой окрестности функция / ( г) других нулей, кроме г а, не имеет. [9]

Тогда на дуге l li лежит один лишь ( У, никаких других нулей и единиц, ни одиноких, ни парных, на ней больше нет. [10]

F ( x) называют изолированным, если в достаточно малой окрестности XQ нет других нулей. [11]

Но тогда существует такая окрестность точки а, в которой f ( z) не имеет других нулей, кроме а. Этот результат коротко формулируют так: если f ( z) аналитична в своих нулях, то эти нули - точки, изолированные друг от друга. [12]

Можно выразить симметрические функции нулей многочлена Л через сумму и произведение х и х2 с одной стороны, и двух других нулей с другой. [13]

Строго возрастающая функция ф не может иметь на [ и0, ut ] более одного нуля, а поскольку XQ является нулем, то других нулей нет. [14]

Можно доказать, что если нуль z0 лежит в области аналитичности f ( z), то существует такая окрестность го, в которой нет других нулей этой функции. [15]

Страницы: 1 2 3