Кратный нуль

Cтраница 2

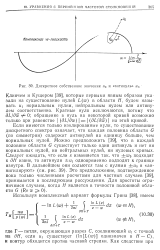Дискретное собственное значение и0 и антипуль и. [16]

Кратные нули исключаются, потому что dL / dw Ф 0; обращение в нуль на некоторой кривой возможно только при равенстве ( dL / dw) ( dL / dw) на этой кривой. [17]

Комплексные нули. [18]

Алгебраический знак каждого измеренного отрезка определяется углом между положительным направлением действительной оси и линией, соединяющей интересующий нас полюс с другим полюсом или нулем. Если имеется кратный нуль, то, для того чтобы определить соответствующий знак, следует угол между кратным нулем и интересующим нас полюсом умножить на число, равное порядку кратности. Применение уравнения ( 23 - 42) поясняется следующим примером. [19]

Диаграмма расположения нулей и полюсов. [20]

Числитель равен единице в случае, если нет нулей, а знаменатель равен единице в случае, если имеется простой полюс. Если на действительной отрицательной оси имеются кратные нули, то расстояние от кратного нуля до исследуемого полюса умножается на число, равное порядку кратности. [21]

Есть гипотеза, что все р являются однократными. Доказаны теоремы о том, что кратных нулей существенно меньше, чем однократных. Есть также гипотеза, что г ( Т) - оо при Т - оо. [22]

В табл. 4.2 приведены рабочие формулы для расчета дисперсии выходного шума а2 для ЦФ с различными передаточными функциями. Из анализа таблицы видно, что введение в передаточную функцию ЦФ простого или кратных нулей в точке z 0 не влияет на величину составляющей дисперсии шума квантования сигнала на выходе ЦФ. Для ЦФ с двумя нулями ( z 1) значение а2 индифферентно к угловому расположению полюсов и определяется лишь их расстояниями до единичной окружности. [24]

Комплексные нули. [25]

Полюс, соответствующий члену 1 / s, является полюсом в начале координат. Пара нулей ju является сопряженными нулями на мнимой оси. Кратные нули и полюсы, не показанные на рисунке, появляются тогда, когда два или более нулей совпадают или когда совпадают два или более полюсов. [27]

Все слагаемые этого выражения являются сопротивлениями некоторых двухполюсников, соединенных последовательно. Однако в слагаемом с коэффициентом Bk степени числителя и знаменателя отличаются на три единицы. Следовательно, предположение о допустимости кратных полюсов сопротивления ( кратных нулей проводимости) является неверным. [28]

Изучены свойства фундаментальных систем решений ( см. стр. Изучены специфические свойства решений уравнений с запаздыванием. Главным внутренним специфическим свойством решений уравнений рассматриваемого вида с запаздыванием являются кратные нули ( если принадлежащие рассматриваемому двумерному подпространству нетривиальные решения уравнения ( 88) с запаздыванием не имеют кратных нулей, то это подпространство является пространством решений некоторого линейного однородного дифференциального уравнения второго порядка без запаздывания с непрерывными коэффициентами - теорема об эквивалентном уравнении без запаздывания - ср. Изучена структура множества нулей решений. Показано, что множество нулей решения уравнения ( 88) может иметь структуру, допустимую для произвольного замкнутого множества. [29]

Поэтому выполним решение для этого случая еще раз, и при этом полностью. Этот способ применим и к разностным уравнениям более высоких порядков, однако тогда необходимо особо рассматривать случай, когда многочлен р ( г) имеет кратные нули. Кроме того, этот способ покажется некоторым читателям более легким, чем способ, изложенный в предыдущем параграфе. [30]

Страницы: 1 2 3