Большая Энциклопедия Нефти и Газа

Если Вас уже третий рабочий день подряд клонит в сон, значит сегодня среда. Законы Мерфи (еще...)

Область - фазовая плоскость

Cтраница 1

Область фазовой плоскости / /, расположенная выше и ниже сепаратрисы, соответствует круговращению маятника.  [1]

Фазовая диаграмма колебаний в часах ( случай единственного стационарного режима.  [2]

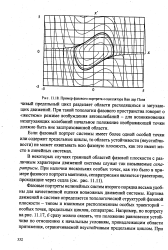
Область фазовой плоскости вне предельного цикла характеризует состояния системы, при которых Л ( 5) Л ( 5) и pS 0, и соответственно заполнена свертывающимися спиральными траекториями, наматывающимися снаружи на предельный цикл.  [3]

Свойства плазмы в некоторой области фазовой плоскости плотность - температура определяются помимо прочих факторов образованием связанных состояний ( см. гл. Обобщения на случаи более сложных комплексов, таких как молекулы или биэкситоны, проводятся непосредственно. Основной результат, получаемый в разд.  [4]

Пример фазового портрета о сциллятора Ван дер Поля чивый предельный цикл разделяет области расходящихся и затухающих движений. При такой топологии фазового пространства говорят о жестком режиме возбуждения автоколебаний - для возникновения незатухающих колебаний начальное положение изображающей точки должно быть вне заштрихованной области.  [5]

В некоторых случаях границей областей фазовой плоскости с различным характером движений системы служат так называемые сепаратрисы.  [6]

Пуанкаре ( область G соответствует области G фазовой плоскости), расположена одна особая точка ( конец оси у), являющаяся седлом. Сепаратриса, выходящая из этого седла, проходит внутри G; сепаратрисой, входящей в седло, является дуга экватора. Все фазовые траектории, попадающие на границы области G, являются входящими в эту область.  [7]

Пуанкаре ( область G соответствует области G фазовой плоскости), расположена одна особая точка ( конец оси г /), являющаяся седлом. Сепаратриса, выходящая из этого седла, проходит внутри G; сепаратрисой, входящей в седло, является дуга экватора. Все фазовые траектории, попадающие на границы области G, являются входящими в эту область.  [8]

Областью притяжения устойчивого предельного цикла называют область па фазовой плоскости, где изображающие точки движутся по фазовым траекториям, навиваясь на данный устойчивый предельный цикл.  [9]

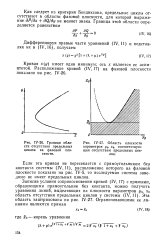Граница области отсутствия предельных циклов на фазовой плоскости.  [10]

Как следует из критерия Бендиксона, предельные циклы отсутствуют в области фазовой плоскости, для которой выражение дР / дх dQ / dy не меняет знака.  [11]

Отсюда, в частности, следует, что если в некоторой области фазовой плоскости нет особых точек дифференциальной системы, то в этой обласги нет и замкнутых траекторий.  [12]

Мы уже знаем, что в случае особой точки типа центра некоторая область фазовой плоскости сплошь заполнена замкнутыми траекториями. Последний случай непосредственно связан с решением вопроса о существовании изолированных периодических решений. При этом интересно, что изолированные замкнутые траектории могут иметь только нелинейные дифференциальные уравнения и системы.  [13]

Направляющая функция на фазовой плоскости.  [14]

Как и при изучении функции Ляпунова, полезно для направляющей функции Е1 определить область фазовой плоскости / где производная по времени отрицательна.  [15]

Страницы:      1    2    3