Область - расстояние
Cтраница 1
Область асимптотических расстояний, на которых действуют дисперсионные силы, дает, таким образом, уникальную возможность строгого решения задачи в рамках теории систем с бесконечным числом взаимодействующих степеней свободы. [1]
Эта область расстояний представляет собой, как принято говорить, потенциальный барьер на пути частицы. Согласно законам классической физики, потенциальный барьер неодолим. Квантовая механика допускает прохождение частицы сквозь потенциальный барьер. [2]
Для каждой области расстояний характерны свои расчетные приближения, позволяющие выделить различные типы взаимодействий и оценить их вклад в межмолекулярный потенциал. В области / 7 /, где межмолекулярные взаимодействия малы, а обмен электронов пренебрежим, справедлива стандартная теория возмущений Релея - Шредингера. Первый порядок теории возмущений дает энергию прямого электростатического взаимодействия систем молекулярных зарядов. Последующие порядки теории возмущений дают поляризационную энергию, появляющуюся вследствие поляризации одной молекулой электронного облака другой. Во втором порядке теории возмущений поляризационная энергия может быть подразделена на индукционную и дисперсионную. В более высоких порядках такое деление уже не может быть проведено. [3]
В этой области расстояний кроме дипольного члена необходимо учесть еще и более высокие члены мультипольного разложения энергии дисперсионного взаимодействия, а также энергию сил отталкивания, возникающих из-за перекрывания электронных облаков взаимодействующих подсистем. [4]
Определение размеров областей когерентного расстояния L согласно методике, описанной в работе [52], проводилось методом аппроксимаций на основе анализа формы и ширины линий ( lll) oii ( 200) никеля. Эталоном служил отожженный при 450 С в течение 4 часов порошок никеля со средним размером частиц 50 мкм. [5]
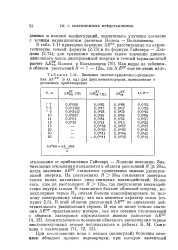 |
Значения синглет-тридлетногорасщепления AEST ( в ат. ед. для двух атомов водорода, вычисленные в различных приближениях. [6] |
Значительные отклонения появляются в области расстояний R 20ао, когда значения & EST становятся существенно меньше дисперсионной энергии. [7]
Поэтому фактически интеграл определяется областью расстояний, лежащих в инерционной области ( Ао С г С /), так что можно подставить в него Brr ( r) из (34.40), распространив в то же время интегрирование по всему пространству. [8]
Поэтому фактически интеграл определяется областью расстояний, лежащих в инерционной области ( Х0 г /), так что можно подставить в него Brr ( r) из ( 34 40), распространив в то Же время интегрирование по всему пространству. [9]
Поэтому фактически интеграл определяется областью расстояний, лежащих в инерционной области ( Хо - С г /), так что можно подставить в него Brr ( r) из ( 34 40), распространив в то же время интегрирование по всему пространству. [10]
Возможность рассмотрения дисперсионного взаимодействия в области расстояний R R и его описания на этих расстояниях на основе результатов, относящихся к взаимодействию атомов в области R Rm, объясняется следующим. Энергия взаимодействия между атомами остается значительно меньше энергии связи электронов в атомах на расстояниях R ( 2 - 2 5) А. При этом атомы еще сохраняют свою индивидуальность, и межатомное взаимодействие можно рассматривать как возмущение. А в виде суммы нескольких членов, каждый из которых допускает сравнительно простую физическую интерпретацию. [11]
Условие (5.30) гарантирует преобладание вклада области расстояний порядка гс во все флуктуационные средние Гя-Это условие выделяет сильно флуктуирующие величины. Поля А, связанные со слабо флуктуирующими величинами ( AAd), не вносят существенных вкладов на больших расстояниях. [12]
Это состояние является отталкивательным за исключением области расстояний, в которой превалируют дисперсионные силы. Взаимодействия такого типа не приводят к образованию стабильных молекул и поэтому не могут быть изучены спектроскопическими методами. Выполнение же достаточно строгих квантово-механических расчетов чрезвычайно сложно. [13]
В случае кулоповского потенциала Ze lr нельзя выделить область расстояний, где потенциал значительно больше, чем в по этой области. Ограничения на углы пет для обоих приближений, дающих, кстати, одинаковые результаты. [14]
Следует подчеркнуть, что мультипольные ван-дер-ваальсовьг силы в области расстояний R K0 очень малы и требуемая для их экспериментального изучения точность измерений пока не достигнута. Это относится как к отдельным атомам, так и к макроскопическим конденсированным частичкам, в частности, с характерным размером а Ю2 А. [15]
Страницы: 1 2 3 4