Область - допустимое управление
Cтраница 1
 |
Схема нагрева и черновой прокатки. [1] |
Область допустимых управлений определена ограничениями на усилия и моменты прокатки, мощность главного привода клетей, а также условиями захвата металла валками и длиной межклетевых рольгангов. [2]
 |
Схема, в которой оптимальное управление не является ни стационарной точкой, ни точкой локального максимума.| К примеру 2. [3] |
На рис. 60 область допустимых управлений представляет собой внешность круга. [4]
Ограничения (V.34) задают область допустимых управлений / с-го блока, в том числе - допустимые сроки останова оборудования на ремонт. Эти последние ограничения, устанавливающие допустимую область для переменных 6, определяются действующей на предприятии системой ППР [50], регламентирующей способ определения диапазона допустимых дат остановки на ремонт. [5]
Принадлежность 3 к области допустимых управлений Qp связана прежде всего с ограниченными возможностями преобразователя частоты по мощности. В зависимости от того, лежит решение задачи на границе области йр или нет, различают безусловную и условную задачи оптимизации. [6]
Таким образом, по критерию QJ формируется область допустимых управлений. В данной области принятые стратегии управления, выраженные парами ( а /, Я), равнозначны. [7]
 |
Схема ( а и геометрическая интерпретация ( б САС рас. [8] |
В главе IV показано, что при увеличении Fp и хр области допустимых управлений сдвигаются вправо и вверх; при увеличении q область допустимых управлений сдвигается вправо. [9]
Рассматривается решение класса задач, в которых целевая функция линейна а область допустимых управлений выпукла. В качестве целевой функции могут быть выбраны себестоимость получения дистиллята или остатка, производительность колонны по дистилляту или остатку, доход. [10]
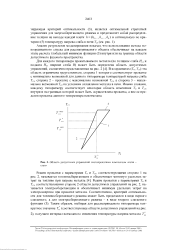 |
Область допустимых управлений листопрокатным комплексом печи - стан. [11] |
Режим прокатки с параметрами Т и Тсл, соответствующими стороне 2 области допустимых управлений на рис. 2, называется электросберегающим и обеспечивает минимум удельных затрат на электроэнергию при прокатке металла. [12]
Из (8.118) следует, что оптимальному управлению соответствуют вершины прямоугольника, ограничивающего область допустимых управлений на плоскости с координатами иг, иг. [13]
Из (11.12) видно, что управление является кусочно-постоянной функцией со значениями на границе области допустимых управлений. [14]
 |
Пространственно-временная модель возникновения и развития нештатных ситуаций. [15] |
Страницы: 1 2 3